벡터공간의 부분집합,subset이 벡터공간의 성질을 가질 경우(...의 공리를 모두 만족할 경우) 부분공간이라고 불러주는 것? chk
대충: (벡터공간,vector_space의 부분집합이?) 두 가지 조건 - vector_addition에 대해 닫혀 있고, scalar배에 대해 닫혀 있으면 부분공간.
정의:
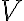 는 적어도 두 부분공간을 가진다.
는 적어도 두 부분공간을 가진다.
집합 V를 벡터공간이라 하고 W(≠0)를 V의 부분집합이라 하자.
이 때, 벡터공간 V에서 정의된 덧셈과 스칼라배에 관하여 W가 벡터공간을 이룰 때,
W를 V의 부분공간(subspace)이라고 한다.
정의 (Zill Defintion 7.6.2)이 때, 벡터공간 V에서 정의된 덧셈과 스칼라배에 관하여 W가 벡터공간을 이룰 때,
W를 V의 부분공간(subspace)이라고 한다.
If a subset 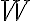 of a vector space
of a vector space 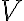 is itself a vector space under the operations of vector addition and scalar multiplication defined on
is itself a vector space under the operations of vector addition and scalar multiplication defined on 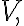 then
then 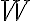 is called a subspace of
is called a subspace of 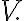
벡터공간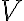 의 부분집합
의 부분집합 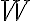 가 그 자체로
가 그 자체로 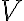 위에서 정의된 벡터 덧셈과 스칼라곱에 대하여 벡터공간이 되면,
위에서 정의된 벡터 덧셈과 스칼라곱에 대하여 벡터공간이 되면, 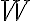 를
를 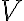 의 부분공간이라 한다. (ko)
의 부분공간이라 한다. (ko)
모든 벡터공간 벡터공간
자체
- zero subspace
...이건 명백히 영공간,null_space과 다름. btw, QQQ 영부분공간,zero_subspace라는 페이지 만들 필요 있나 없나?
이건 스칼라배에 대해 닫혀있어야 하므로 - 따라서 0의 곱셈에 대해서도 닫혀있어야 하므로 - 자명하게 나오는 성질? ... 정의 중 하나인지 아님 성질인지? chk
QQQ linear_subspace와 정확히? subspace의 일종이 linear_subspace인지, 아님 항상 동의어인지, 아님 linalg 범위 내에서는 항상 동의어이고 밖에선 다를 수 있는 것인지, ... curr see  Linear_subspace
Linear_subspace  Linear subspace
Linear subspace
Sub:
벡터공간,vector_space에는 그 부분공간이 있을수 ... 항상?
생성,span
영공간,null_space
열공간,column_space
행공간,row_space
http://mlwiki.org/index.php/Four_Fundamental_Subspaces
밀접, 관계 tbw.열공간,column_space
행공간,row_space
http://mlwiki.org/index.php/Four_Fundamental_Subspaces
벡터공간,vector_space에는 그 부분공간이 있을수 ... 항상?
생성,span
1. 정의 ¶
(생각) 그럼 대충 이런듯. 부분공간이란,
- 벡터공간의 부분집합
- 공집합은 아님
- 그 자체로도 벡터공간이어야 함
W is a subspace of V iff W satisfies
① u,v ∈ W ⇒ u+v ∈ W
② c scalar, u ∈ W ⇒ cu ∈ W
① u,v ∈ W ⇒ u+v ∈ W
② c scalar, u ∈ W ⇒ cu ∈ W
부분공간의 판정 기준
벡터공간,vector_space V의 공집합,empty_set이 아닌 부분집합,subset W가 부분공간이 되기 위한 필요충분조건은 W가 V에서 정의된 벡터 덧셈과 스칼라곱에 대해 닫혀 있을 때이다.
벡터공간,vector_space V의 공집합,empty_set이 아닌 부분집합,subset W가 부분공간이 되기 위한 필요충분조건은 W가 V에서 정의된 벡터 덧셈과 스칼라곱에 대해 닫혀 있을 때이다.
- x와 y가 W 안에 있을 때 x+y도 W 안에 있다.
- x가 W 안에 있고, k가 임의의 스칼라이면, kx는 W 안에 있다.
(차원,dimension, 기저,basis, 생성,span을 설명하고 바로 뒤에)
벡터공간 V의 공집합이 아닌 부분집합으로, 그 자체가 벡터공간인 경우 (V에서 정의된 덧셈과 스칼라곱을 가지고), 이를 벡터공간 V의 부분공간(subspace)이라고 한다.
(Kreyszig 7.4 벡터공간)
벡터공간 V의 공집합이 아닌 부분집합으로, 그 자체가 벡터공간인 경우 (V에서 정의된 덧셈과 스칼라곱을 가지고), 이를 벡터공간 V의 부분공간(subspace)이라고 한다.
(Kreyszig 7.4 벡터공간)
2. 설명 ¶
예 (최도훈)
W5 : the vector space of all functions on [0,1]
W4 : the set of all integrable functions on [0,1]
W3 : the set of all continuous functions on [0,1]
W2 : the set of all differentiable functions on [0,1]
W1 : the set of all polynomials on [0,1]
여기서, W5 ⊃ W4 ⊃ W3 ⊃ W2 ⊃ W1이라고.W4 : the set of all integrable functions on [0,1]
W3 : the set of all continuous functions on [0,1]
W2 : the set of all differentiable functions on [0,1]
W1 : the set of all polynomials on [0,1]
Thm.
V : 한 벡터공간
U and W : V의 부분공간
⇒U and W : V의 부분공간
U ∩ W 는 V의 부분공간
즉 subspace의 교집합은 다시 subspace. (증명은 어렵지 않다는데 생략, 찾으려면 see 소스) 3.1. Khan Academy: Lin Alg: Linear Subspaces ¶
V subspace of ℝn:
V contains zero vector
V contains zero vector
일단 closure(폐포, 닫힘)이란 단어가 나온다. 집합론/군론의 closed랑 호환되는 거겠지 아마..
x in V → cx in V : closure under scalar multiplication
a in V, b in V → a+b in V : closure under addition
x in V → cx in V : closure under scalar multiplication
a in V, b in V → a+b in V : closure under addition
이상 세 가지 조건을 만족하면 subspace? CHK
- 영벡터가 있다 (덧셈의 항등원)
- 스칼라곱에 닫혀 있다
- 덧셈에 닫혀 있다
3.3. 행공간, 열공간, 영공간 ¶
이것들은 모두 벡터공간, 부분공간?
A를 m×n행렬이라 할 때
A의 행벡터 r1, r2, …, rm이 생성하는 ℝn의 subspace를 A의 행공간(row space)이라 함. 행공간,row_space
A의 열벡터 c1, c2, …, cn이 생성하는 ℝm의 subspace를 A의 열공간(column space)이라 함. 열공간,column_space
ℝn의 subspace의 동차연립방정식 Ax=0의 해로 이루어진 공간을 영공간(null space)이라 함. 영공간,null_space
A의 행벡터 r1, r2, …, rm이 생성하는 ℝn의 subspace를 A의 행공간(row space)이라 함. 행공간,row_space
A의 열벡터 c1, c2, …, cn이 생성하는 ℝm의 subspace를 A의 열공간(column space)이라 함. 열공간,column_space
ℝn의 subspace의 동차연립방정식 Ax=0의 해로 이루어진 공간을 영공간(null space)이라 함. 영공간,null_space
비동차연립일차방정식 Ax=b의 일반해는, 동일한 A를 가지는 Ax=0의 일반해,general_solution에, 특수해,particular_solution를 추가해 얻을 수 있다고. //todo: 해,solution에서 이곳 link
위에서 언급했듯, A의 영공간은 Ax=0의 해공간.
만약 x0가 비동차연립일차방정식 Ax=b의 어떤 해이고,
S={v1, v2, ..., vk}가 A의 영공간의 기저,basis라면,
Ax=b의 모든 해는 다음 형태로 표현 가능:
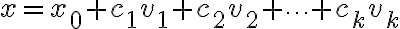
x는 Ax=b의 일반해,general_solution가 되고,
x0는 Ax=b의 특수해,particular_solution이며,
위의 x에서 x0를 제외한 나머지 부분은 Ax=0의 일반해라고 한다.
위에서 언급했듯, A의 영공간은 Ax=0의 해공간.
만약 x0가 비동차연립일차방정식 Ax=b의 어떤 해이고,
S={v1, v2, ..., vk}가 A의 영공간의 기저,basis라면,
Ax=b의 모든 해는 다음 형태로 표현 가능:
x0는 Ax=b의 특수해,particular_solution이며,
위의 x에서 x0를 제외한 나머지 부분은 Ax=0의 일반해라고 한다.
결론:
비동차연립일차방정식의 일반해는, 그 연립방정식의 특수해와 동차연립방정식의 일반해의 합이다.
비동차연립일차방정식의 일반해는, 그 연립방정식의 특수해와 동차연립방정식의 일반해의 합이다.
3.4. 8.pdf ¶
Excerpts from http://elearning.kocw.net/contents4/document/lec/2013/Chungbuk/LeeGeonmyeong1/8.pdf
{
Summary:
{
Summary:
- 부분공간은, 벡터공간의 성질을 만족하는, 공간의 부분집합이다.
- 주요 부분공간: 영공간, 열공간, 행공간, 좌영공간
- 영공간은 동차선형시스템(homogeneous 선형방정식,linear_equation) Ax=0의 모든 해의 집합.
- 열공간은 주어진 행렬에 대한 열벡터들의 모든 선형결합의 집합.
- 행공간은 주어진 행렬에 대한 행벡터들의 모든 선형결합의 집합.
- 좌영공간은 전치행렬,transpose_matrix의 영공간,null_space
영부분공간(zero subspace):
행렬 A의 열벡터들의 모든 선형결합의 집합.
기호: Col(A)
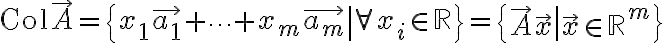
// A, x 위에 화살표 맞는지, R이 실수집합 맞는지, chk....
영벡터만으로 구성된 집합 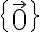
행렬 A의 열공간(column space, range, image):행렬 A의 열벡터들의 모든 선형결합의 집합.
기호: Col(A)
(저 밑에부터는 괄호를 안 적었는데 별 상관은 없겠지....)
// A, x 위에 화살표 맞는지, R이 실수집합 맞는지, chk....
행렬 A의 행공간(row space)
기호: Row A
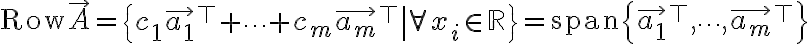
// x_i는 c_i 아닌가? 바로 밑에 나온 것처럼.
기호: Row A
// x_i는 c_i 아닌가? 바로 밑에 나온 것처럼.
행공간과 영공간의 직교.
\vec{x}=c_1\vec{a_1}{}^{\top}\vec{x}+\cdots+c_m\vec{a_i}{}^{\top}\vec{x}=0)
즉 (행공간벡터)(영공간벡터 x) = 0
// 끝에 a_i는 a_m 아닌가??
행공간 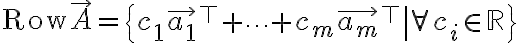
영공간 Ax=0
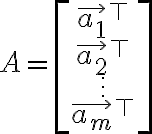
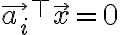
식으로영공간 Ax=0
즉 (행공간벡터)(영공간벡터 x) = 0
// 끝에 a_i는 a_m 아닌가??
추축열(pivotal column):
행사다리꼴에서 추축(pivot)을 갖는 행렬의 열.
행렬 A의 추축열들은 열공간(column space)의 기저가 된다.
//주축열이라고 하는 곳도 있던데
행사다리꼴에서 추축(pivot)을 갖는 행렬의 열.
행렬 A의 추축열들은 열공간(column space)의 기저가 된다.
//주축열이라고 하는 곳도 있던데
기저,basis 생략.
좌표,coordinate 생략.
차원,dimension 생략.
계수,rank
계수 정리(rank theorem), rank-nullity thm
행렬 A가 n개의 열을 가지면
rank A = rank AT 생략.
가역행렬정리 생략.
}
계수 정리(rank theorem), rank-nullity thm
행렬 A가 n개의 열을 가지면
rank A + dim Nul A = n
여기서dim Nul A (= A의 nullity) : 자유변수(free variable) 개수
rank A : 추축열(pivotal column) 개수
left nullspace 생략.rank A : 추축열(pivotal column) 개수
rank A = rank AT 생략.
가역행렬정리 생략.
}
4. 인터넷 페이지들 요약 CHK MERGE DELME ¶
CHK, 인터넷 포스팅 등을 참조하였음. 확인 후 본문에 merge.
{
선형결합으로 이루어지는 공간이 1. 원점을 지나고 2. 덧셈 연산에 닫혀있는 경우, 부분 공간(subspace)이 될 수도 있다.
V와 W는 벡터공간이고, V가 W의 부분집합이면, V는 W의 부분공간(subspace)이라고 한다.
다시 정리하면, 벡터공간 V의 부분집합인 H가 다음을 만족할 때 부분공간(subspace)이라고 한다.
{
선형결합으로 이루어지는 공간이 1. 원점을 지나고 2. 덧셈 연산에 닫혀있는 경우, 부분 공간(subspace)이 될 수도 있다.
V와 W는 벡터공간이고, V가 W의 부분집합이면, V는 W의 부분공간(subspace)이라고 한다.
다시 정리하면, 벡터공간 V의 부분집합인 H가 다음을 만족할 때 부분공간(subspace)이라고 한다.
- V에 속하는 영벡터(zero vector)가 H의 원소이다.
- u,v∈H, u+v∈H, v+u∈H
- u∈H이고 임의의 스칼라 c에 대해 cu∈H
벡터공간 V의 부분집합인 H가 다음을 만족할 때 부분공간(subspace)이라고 합니다.
(1) V에 속하는 영벡터(zero vector)가 H의 원소이다.
(2) u,v∈H, u+v∈H, v+u∈H
(3) u∈H이고 임의의 스칼라 c에 대해 cu∈H
(페이지에 그림 있음)
// https://ratsgo.github.io/linear algebra/2017/05/20/spaces/
(1) V에 속하는 영벡터(zero vector)가 H의 원소이다.
(2) u,v∈H, u+v∈H, v+u∈H
(3) u∈H이고 임의의 스칼라 c에 대해 cu∈H
(페이지에 그림 있음)
// https://ratsgo.github.io/linear algebra/2017/05/20/spaces/
정의
 상의 부분공간의 예.
상의 부분공간의 예.
 가
가  상의 벡터일 때, 모든 일차결합
상의 벡터일 때, 모든 일차결합
들의 집합은  상의 부분공간이 된다.
상의 부분공간이 된다.
이렇게 만들어진  상의 부분공간
상의 부분공간 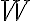 를,
를,
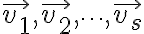 의 생성,span이라 하며 다음과 같이 표기.
의 생성,span이라 하며 다음과 같이 표기.
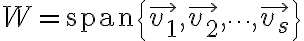
혹은 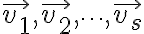 가
가 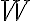 를 생성한다고 함.
를 생성한다고 함.
 는 매개변수(parameters).
는 매개변수(parameters).
공집합이 아닌  상의 벡터들의 집합이,
상의 벡터들의 집합이,
스칼라곱과 덧셈에 닫혀있다면,
(i.e. 일차결합=선형결합,linear_combination에 대하여 닫혀있다면,)
이것을 상의 부분공간이라 한다.
상의 부분공간이라 한다.
스칼라곱과 덧셈에 닫혀있다면,
(i.e. 일차결합=선형결합,linear_combination에 대하여 닫혀있다면,)
이것을
영부분공간(zero subspace) : 영벡터만을 원소로 가짐. 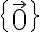
 그 자체
그 자체
 상의 벡터의 스칼라곱은
상의 벡터의 스칼라곱은  상의 벡터가 되며
상의 벡터가 되며
 상의 두 벡터의 합은
상의 두 벡터의 합은  상의 벡터가 되므로.
상의 벡터가 되므로.
(위 둘은 자명한 부분공간(trivial subspace).)
정의(2)영벡터의 스칼라곱과 두 영벡터의 합은 영벡터이므로,  상의 부분공간임.
상의 부분공간임.
정리:
임의의 의 부분공간은 반드시 zero vector를 포함해야 한다.
의 부분공간은 반드시 zero vector를 포함해야 한다.
임의의
아래에서 영벡터(zero vector)=원점(origin) 혼용됨. 일부러 혼용함 - 여기서 완전히 같은 뜻인듯.
전체
- 영벡터를 지나는 임의의 직선,line - 원점을 지나는 아무 직선
- 영벡터 only - 영벡터 그 자체
- {(0,0)}
- a line passing through (0,0)
행렬의 부분공간(subspace of matrix)
에는 여러가지가 있을텐데 (행공간 등등?)....
바로 열공간,column_space을 뽑아낼 수 있다
임의의 행렬 A에서, 모든 열,column의 선형결합,linear_combination은 부분공간(subspace)을 형성한다.
이것을 column space라 부르고
C(A)로 쓴다.
임의의 행렬 A에서, 모든 열,column의 선형결합,linear_combination은 부분공간(subspace)을 형성한다.
이것을 column space라 부르고
C(A)로 쓴다.
벡터공간 V의 부분집합 W가 있다.
W는 공집합이 아니다.
V상에서 정의된 덧셈과 스칼라곱에 대해 벡터공간,vector_space이 될 때,
(i.e. 벡터공간의 열 공리를 만족할 때)
W를 벡터공간 V의 부분공간이라 한다. 표기는:
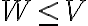
어떤 부분공간들의 합집합(∪)은 부분공간이 아니다. (QQQ 즉, 항상 아니라는 뜻?)
어떤 부분공간들의 교집합(∩)은 부분공간이다.
W는 공집합이 아니다.
V상에서 정의된 덧셈과 스칼라곱에 대해 벡터공간,vector_space이 될 때,
(i.e. 벡터공간의 열 공리를 만족할 때)
W를 벡터공간 V의 부분공간이라 한다. 표기는:
어떤 부분공간들의 교집합(∩)은 부분공간이다.
2D 벡터공간의 부분공간:
- 그 전체
- 원점(zero vector)
- 원점을 지나는 모든 직선
- 그 전체
- 원점(zero vector)
- 원점을 지나는 모든 직선
- 원점을 지나는 모든 평면
- 벡터 합이 부분공간 내에 있어야 (즉 닫혀있다)
- 벡터의 실수배가 부분공간 내에 있어야
- 원점을 반드시 포함해야 (즉 실수배에서 실수가 0인 경우)
- 원점을 반드시 포함해야 (즉 실수배에서 실수가 0인 경우)
3D 벡터공간에 원점을 지나는 직선(L)과 평면(P)가 있다고 가정. L은 P위에 있지 않다. 교차점은 원점 뿐이다.
그러면 다음은 부분공간인가?
P∪L
그러면 다음은 부분공간인가?
P∪L
no. 합 결과가 P, L을 모두 벗어날 수 있다.
P∩Lyes. 원점뿐이므로.
열공간,column_space 생략}
Twins:
![[https]](/123/imgs/https.png) 수학백과: 부분공간
수학백과: 부분공간
https://proofwiki.org/wiki/Definition:Subspace (Disambiguation) ▶ https://proofwiki.org/wiki/Definition:Vector_Subspace
https://planetmath.org/vectorsubspace
https://everything2.com/title/Subspace
![[https]](/123/imgs/https.png) 수학백과: 부분공간
수학백과: 부분공간https://proofwiki.org/wiki/Definition:Subspace (Disambiguation) ▶ https://proofwiki.org/wiki/Definition:Vector_Subspace
https://planetmath.org/vectorsubspace
https://everything2.com/title/Subspace


![[http]](/123/imgs/http.png)