sin과 cos의 가중합,weighted_sum?
기저,basis를 단순하게
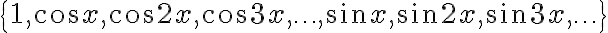 로 두면 범위가
로 두면 범위가 ![$[-\pi,\pi]$ $[-\pi,\pi]$](/123/cgi-bin/mimetex.cgi?\Large [-\pi,\pi]) 로 고정되어 버린다.
로 고정되어 버린다.
![$[-T,T]$ $[-T,T]$](/123/cgi-bin/mimetex.cgi?\Large [-T,T]) 범위의 임의의 주기,period ( 즉 주기의 길이는
범위의 임의의 주기,period ( 즉 주기의 길이는 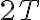 ) 를 쓰려면 삼각함수 속
) 를 쓰려면 삼각함수 속 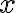 앞의 계수
앞의 계수 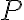 가
가 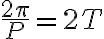 즉
즉 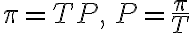 이면 되므로 기저를
이면 되므로 기저를
,\cos\left(\frac{2\pi}{T}x\right),\cos\left(\frac{3\pi}{T}x\right),\ldots,\sin\left(\frac{\pi}{T}x\right),\sin\left(\frac{2\pi}{T}x\right),\sin\left(\frac{3\pi}{T}x\right),\ldots\right}) 로 하면 반복되는 범위를
로 하면 반복되는 범위를 ![$[-T,T]$ $[-T,T]$](/123/cgi-bin/mimetex.cgi?\Large [-T,T]) 로 일반화할 수 있다.
로 일반화할 수 있다.
그리고 저 집합 직교성,orthogonality을 가짐. ∫sin()cos()dx 뿐만 아니라 ∫cos()cos()dx도 마찬가지로 0이 나오는.
// tmp from https://youtu.be/XwsPTAnFRsk
여기서 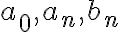 은 다음 공식으로 구한다.
은 다음 공식으로 구한다.
dx)
\cos\left(\frac{n\pi}{L}x\right)dx)
\sin\left(\frac{n\pi}{L}x\right)dx)
// tmp from https://youtu.be/DVlSETdpEao
푸리에에 의하면, 모든 주기함수,periodic_function는 사인 함수와 코사인 함수의 (무한)합으로 나타난다. 함수
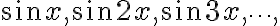
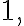
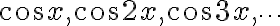
는 모두 주기,period가  인 함수이다. (주기는 "최소 주기"를 뜻하기도 하지만 여기서는 넓은 의미로 사용하였다.) 함수
인 함수이다. (주기는 "최소 주기"를 뜻하기도 하지만 여기서는 넓은 의미로 사용하였다.) 함수 ) 가 주기가
가 주기가  인 함수이면,
인 함수이면,
=a_0+\sum_{n=1}^{\infty}\left( a_n \cos nx + b_n \sin nx \right))
를 만족시키는 실수 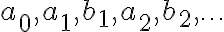 가 (오직 하나) 존재한다. 이 때 위 식의 오른쪽 항을
가 (오직 하나) 존재한다. 이 때 위 식의 오른쪽 항을  의 푸리에 급수라고 부른다.
의 푸리에 급수라고 부른다.
(김홍종 미적1+ p141)
(정의) Fourier 급수
구간) 에서 정의된 함수
에서 정의된 함수  의 Fourier 급수는 다음과 같다.
의 Fourier 급수는 다음과 같다.
=\frac{a_0}{2}+\sum_{n=1}^{\infty}\left( a_n\cos\frac{n\pi}{p}x + b_n\sin\frac{n\pi}{p}x \right))
여기서
\,dx)
\cos\frac{n\pi}{p}x\,dx)
\sin\frac{n\pi}{p}x\,dx)
이다.
구간
(Zill 8e ko vol2 p12)
trig- 와 expon- 이 있는데.. 관계 정확히
 trigonometric.fourier.series
trigonometric.fourier.series
 exponential.fourier.series
exponential.fourier.series
 trigonometric.fourier.series exponential
trigonometric.fourier.series exponential
일반화,generalization버전? :
generalized_Fourier_series - writing; curr see 일반화된.푸리에급수
일반화된.푸리에급수  generalized.fourier.series
generalized.fourier.series
generalized_Fourier_series - writing; curr see
조화해석,harmonic_analysis : 함수를 푸리에급수 꼴로 나타내는 일. 푸리에급수 전개에서 각 항의 계수를 구하는 기법.
//수백
주어진 구간,interval 내에서 정의된 함수 를 특수한 삼각함수,trigonometric_function의 직교집합,orthogonal_set을 기저,basis로 하여 전개,expansion하는 것.
를 특수한 삼각함수,trigonometric_function의 직교집합,orthogonal_set을 기저,basis로 하여 전개,expansion하는 것.
현대적 관점에선 푸리에 급수를 공간,space의 대칭성,symmetry의 결과로 이해...
주어진 구간,interval 내에서 정의된 함수
현대적 관점에선 푸리에 급수를 공간,space의 대칭성,symmetry의 결과로 이해...
먼저 직교집합을 정의하면 (copied to local)
구간,interval![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) 에서 정의된 실수값 함수들의 집합,set
에서 정의된 실수값 함수들의 집합,set 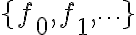 이 다음을 만족하면, 이 집합은 직교집합이다.
이 다음을 만족하면, 이 집합은 직교집합이다.
=\int_a^b f_m(x) f_n(x) dx = 0\;\;\;(m\ne n))
좌변은 내적,inner_product을 뜻한다. 즉 함수의 내적이 0이면 두 함수가 직교한다(직교성,orthogonality)고 정의하는 것.
구간,interval
그다음 삼각급수,trigonometric_series(writing) 매우 길어서 나중에. tbw
tmp from https://www.youtube.com/watch?v=0aSZM7Qj1HY
=\frac{a_0}{2}+\sum_{n=1}^{\infty}a_n\cos\left(\frac{2\pi nx}{T}\right)+\sum_{n=1}^{\infty}b_n\sin\left(\frac{2\pi nx}{T}\right))
식의 의미는 '코사인과 사인을 무한히 섞으면 주기함수를 표현가능하다'
여기서
식의 의미는 '코사인과 사인을 무한히 섞으면 주기함수를 표현가능하다'
여기서
- 맨 앞
: 직류,DC를 표현, - 정적평형,static_equilibrium(see 평형,equilibrium > 물리에서의 평형)
- 나머지 시그마 두개 합 : 교류,AC를 표현. - 진동,oscillation,vibration
연속신호/연속함수는 무한차원벡터이고,
이것은 기저벡터의 선형결합으로 재구성할 수 있다.
이것은 기저벡터의 선형결합으로 재구성할 수 있다.
n차원 벡터는 n개 숫자의 나열이고
함수는 값을 무한 개 나열한 것으로 볼 수 있으므로
함수는 무한 차원 벡터로 생각할 수 있다.
함수는 값을 무한 개 나열한 것으로 볼 수 있으므로
함수는 무한 차원 벡터로 생각할 수 있다.
함수는 무한차원벡터공간의 한 점으로 볼 수 있다.
Def. 함수의 내적(inner product of functions)
The inner product of two functions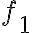 and
and 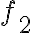 on an interval
on an interval ![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) is the number
is the number
=\int_a^b f_1(x)f_2^*(x)dx)
Def. 직교함수(orthogonal functions)
Two functions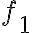 and
and 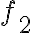 are said to be orthogonal on an interval
are said to be orthogonal on an interval ![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) if
if
=\int_a^b f_1(x)f_2^*(x)dx=0)
Def. 직교 함수 집합, orthogonal set
A set of complex-valued functions,\phi_1(x),\phi_2(x),\cdots\rbrace) is said to be orthogonal on an interval
is said to be orthogonal on an interval ![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) if
if
=\int_a^b \phi_m(t) \phi_n^* (t)dt=0,\;\;\;m\ne n)
(see 내적,inner_product 직교성,orthogonality 직교함수,orthogonal_function. *는 켤레,conjugate)
The inner product of two functions
Two functions
A set of complex-valued functions
위에서 말한 무한개의 직교함수들의 선형결합으로 표현한다는 것을 식으로 나타내면
=c_0\Phi_0(x)+c_1\Phi_1(x)+\cdots+c_n\Phi_n(x)+\cdots)
=\sum_{n=0}^{\infty}c_n\Phi_n(x))
Def. 연속 시간 푸리에 급수 Continous time Fourier series
For any signal) satisfying
satisfying =x(t+T),) we can write
we can write
=\sum_{k=-\infty}^{\infty} a_k \exp\left( j\frac{2\pi k}{T} t \right))
Fourier series는 두 식으로 구성. 아래 두 식은 하나의 신호를 분석하는 두 관점.
(1)
=\sum_{k=-\infty}^{\infty}a_k\exp\left( j\frac{2\pi k}{T}t\right ))
연속신호(=연속함수)는 무한차원벡터이고, 이것은 기저,basis벡터(삼각함수,trigonometric_function)의 선형결합,linear_combination으로 재구성 가능.
(2)
) 이 지수함수는 주파수(진동수,frequency)가
이 지수함수는 주파수(진동수,frequency)가 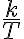 인 삼각함수를 뜻함.
인 삼각함수를 뜻함.
식= -j\sin\left( \frac{2\pi k}{T} t \right)) 이므로.
이므로.
For any signal
(1)
연속신호(=연속함수)는 무한차원벡터이고, 이것은 기저,basis벡터(삼각함수,trigonometric_function)의 선형결합,linear_combination으로 재구성 가능.
식=
정의 5.1: 푸리에 급수
주기,period가  인, 즉 2π-주기 함수
인, 즉 2π-주기 함수 ) 의 푸리에 급수
의 푸리에 급수 ) 를 다음과 같이 정의한다.
를 다음과 같이 정의한다.
=\frac{a_0}{2}+\sum_{n=1}^{\infty}\left( a_n \cos nx + b_n \sin nx \right))
여기서 푸리에_계수,Fourier_coefficients라고 불리는 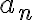 과
과 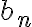 은 다음 식으로 주어진다.
은 다음 식으로 주어진다.
\cos nx\,dx, \;\;\; n=0,1,\cdots)
\sin nx\,dx, \;\;\; n=1,2,\cdots)
(이승준 p85)
복소 푸리에 급수 complex Fourier series ¶
정의 12.4.1 복소 Fourier 급수
구간 ) 에서 정의된 함수
에서 정의된 함수  의 복소 Fourier 급수(complex Fourier series)는 아래와 같이 주어진다.
의 복소 Fourier 급수(complex Fourier series)는 아래와 같이 주어진다.
=\sum_{n=-\infty}^{\infty} c_n e^{in\pi x / p})
여기서
 e^{-in\pi x/p} dx,\; n=0,\pm1,\pm2,\ldots)
이다.
(Zill 8e ko vol2 p26)
bmks ko tmp ¶
bmks en ¶
interactive, demo
https://demonstrations.wolfram.com/ExamplesOfFourierSeries/
https://demonstrations.wolfram.com/FourierSeriesOfSimpleFunctions/
https://demonstrations.wolfram.com/ApproximationOfDiscontinuousFunctionsByFourierSeries/
https://demonstrations.wolfram.com/ComparingFourierSeriesAndFourierTransform/
https://demonstrations.wolfram.com/ExamplesOfFourierSeries/
https://demonstrations.wolfram.com/FourierSeriesOfSimpleFunctions/
https://demonstrations.wolfram.com/ApproximationOfDiscontinuousFunctionsByFourierSeries/
https://demonstrations.wolfram.com/ComparingFourierSeriesAndFourierTransform/
Related:
푸리에_변환,Fourier_transform
{
푸리에 급수 직교성 ... tmp from https://youtu.be/VqeGQkRaSSg?t=75
푸리에_변환,Fourier_transform
푸리에 급수는 주기함수,periodic_function에 대해서만 쓸 수 있고 비주기 함수(aperiodic_function)에 대해서 비슷한 도구가 푸리에 변환.
직교성,orthogonality과의 관계{
푸리에 급수 직교성 ... tmp from https://youtu.be/VqeGQkRaSSg?t=75
적분이 영,zero이 되는.. tbw
아래 둘은 m과 n이 다르면 무조건 0이 나온다. 직교성 때문에. 다시 말해 m과 n이 같다면 '뭔가가 나온다' 는 뜻..(? 정확히)
)
)
3:00~ 나중에 적든지
Twins:
![[https]](/123/imgs/https.png) 두산백과: 푸리에 급수
두산백과: 푸리에 급수
![[https]](/123/imgs/https.png) 수학백과: 푸리에 급수
수학백과: 푸리에 급수
 푸리에_급수
푸리에_급수
{
"주기함수,periodic_function를 삼각함수,trigonometric_function의 가중치(see 가중값,weight)로 분해,decomposition한 급수,series다. 함수의 푸리에 계수,coefficient는 원래 함수보다 다루기 쉽다."
}
 Fourier_series
Fourier_series
 Fourier_sine_and_cosine_series
Fourier_sine_and_cosine_series
http://javalab.org/fourier_series/ (시각화와 간단한 예제)
https://ghebook.blogspot.kr/2012/07/fourier-series.html
https://mathworld.wolfram.com/FourierSeries.html
https://encyclopediaofmath.org/wiki/Fourier_series
![[https]](/123/imgs/https.png) 브리태니커 11e (1911): Fourier's Series
브리태니커 11e (1911): Fourier's Series
https://everything2.com/title/Fourier series
https://en.citizendium.org/wiki/Fourier_series
https://proofwiki.org/wiki/Definition:Fourier_Series
![[https]](/123/imgs/https.png) 두산백과: 푸리에 급수
두산백과: 푸리에 급수![[https]](/123/imgs/https.png) 수학백과: 푸리에 급수
수학백과: 푸리에 급수{
"주기함수,periodic_function를 삼각함수,trigonometric_function의 가중치(see 가중값,weight)로 분해,decomposition한 급수,series다. 함수의 푸리에 계수,coefficient는 원래 함수보다 다루기 쉽다."
}
http://javalab.org/fourier_series/ (시각화와 간단한 예제)
https://ghebook.blogspot.kr/2012/07/fourier-series.html
https://mathworld.wolfram.com/FourierSeries.html
https://encyclopediaofmath.org/wiki/Fourier_series
![[https]](/123/imgs/https.png) 브리태니커 11e (1911): Fourier's Series
브리태니커 11e (1911): Fourier's Serieshttps://everything2.com/title/Fourier series
https://en.citizendium.org/wiki/Fourier_series
https://proofwiki.org/wiki/Definition:Fourier_Series

