| 가우스 면 내부 전하 | 내부 전하의 부호 | 나오는 전기선속 |
| 전하가 없으면 | ||
| 양의 전하가 있으면 | ||
| 음의 전하가 있으면 |
가상의 폐곡면(닫힌 면)
임의로 잡을 수 있음
임의로 잡을 수 있음
따라서 보통 대칭성을 이용할 수 있고 계산이 최소화되는 것을 선택하는 듯..
보통 구면, 정육면체, 원통형(실린더형) 예를 드는 듯..Rel. 가우스_법칙,Gauss_s_law
(전하 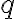 를 둘러싼) 폐곡면을 지나는 알짜선속(전속,electric_flux)은
를 둘러싼) 폐곡면을 지나는 알짜선속(전속,electric_flux)은
- 폐곡면 내부의 전하
에만 의존 (밖의 전하는 신경쓸 필요 X)
- 폐곡면의 모양에 무관
- 크기는
surface대신 shell이라고도 하는 듯
대칭성,symmetry...을 잘 찾아서 가우스면을 잡으면 편하다...던데....
점대칭 point symmetry
선대칭 line symmetry
면대칭 plane symmetry
전기장에 대한 것과 자기장에 대한 것이 있는데 현재 내용은 대부분 전기장에 대한 것이며 자기장에 대한 것은 맨 밑으로.선대칭 line symmetry
면대칭 plane symmetry
다음과 같은 여러 표현이 있음
전속으로 표현하면, 알짜 전하(net charge) qenc가 들어 있는 것(?)의 표면을 알짜 전속(net flux) Φ가 통과? 할때
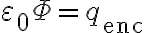
전기장으로 표현하면,
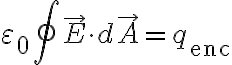
(Halliday 10e)
dA 아닌가? CHK
(Bauer)(진공의 유전율) × (닫힌 곡면에 대한 플럭스) = (닫힌 곡면 안에 든 전하량)
(닫힌 곡면에 대한 플럭스) = (닫힌 곡면 안에 든 전하량) / ε0
가우스 곡면에 대한 플럭스는 전기장의 그 곡면에 대한 면적분,surface_integral으로 주어짐.
닫힌 곡면 S, 그 안의 총 전하량 q, 닫힌 곡면 위 각 지점에서의 전기장 값을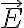 라 하면, 가우스 법칙은
라 하면, 가우스 법칙은
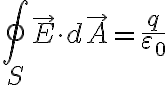
(![[https]](/123/imgs/https.png) 물리산책 가우스의 법칙)
물리산책 가우스의 법칙)
(닫힌 곡면에 대한 플럭스) = (닫힌 곡면 안에 든 전하량) / ε0
가우스 곡면에 대한 플럭스는 전기장의 그 곡면에 대한 면적분,surface_integral으로 주어짐.
닫힌 곡면 S, 그 안의 총 전하량 q, 닫힌 곡면 위 각 지점에서의 전기장 값을
![[https]](/123/imgs/https.png) 물리산책 가우스의 법칙)
물리산책 가우스의 법칙)1. 쿨롱 법칙과의 관계 ¶
쿨롱 법칙을 쓰면 힘든 특별한 문제들을 Gauss법칙으로 쉽게 풀 수 있다.
가우스 법칙에서 쿨롱 법칙을 이끌어내기
점 전하 q가 원점에 있고, 반지름 r인 공 표면에서 전기장 E의 크기는 구의 대칭성 때문에 일정하고, 방향은 밖으로 나아가는 방향, 등을 가정하면 (CHK)
=\frac{q}{\epsilon_0})
따라서

이렇게 쿨롱 법칙이 나옴. See also 쿨롱_법칙,Coulomb_s_law
점 전하 q가 원점에 있고, 반지름 r인 공 표면에서 전기장 E의 크기는 구의 대칭성 때문에 일정하고, 방향은 밖으로 나아가는 방향, 등을 가정하면 (CHK)
2. tocleanup ¶
균일한 전기장 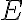 가 있을 때, 이 전기장에 수직이고 면적이
가 있을 때, 이 전기장에 수직이고 면적이  인 면을 지나는 전기장 선속(전기선속, 전속,electric_flux)
인 면을 지나는 전기장 선속(전기선속, 전속,electric_flux) 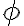 는
는
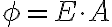
면적  가 전기장
가 전기장 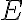 와 수직하지 않을 때, 전기장
와 수직하지 않을 때, 전기장 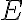 에 수직한 면적
에 수직한 면적 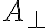 을 지나는 전속과 면적
을 지나는 전속과 면적  를 지나는 전속이 같다.
를 지나는 전속이 같다.
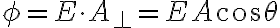
일반적으로는
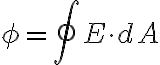
점전하,electric_charge 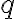 를 중심으로 하는 반지름
를 중심으로 하는 반지름  인 구면을 지나는 전속
인 구면을 지나는 전속 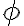 는,
는,
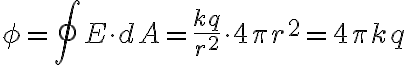
그리고 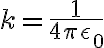 이므로
이므로
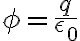
따라서
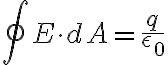
(전기장의 세기) ∝ (단위면적당 전기력선의 수) = (전기력선의 수) / (면적)
즉,
(면적) × (전기장의 세기) ∝ (전기력선의 수)
즉,
(면적) × (전기장의 세기) ∝ (전기력선의 수)
3. 차동우 ¶
폐곡면(가우스 면, 가우스 곡면, 가우스 폐곡면)을 통과하는 전기장,electric_field의 총 선속,flux (i.e. 전속,electric_flux) 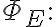
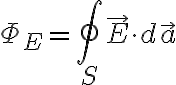
그 폐곡면 내 포함된 알짜전하(+, -을 상쇄하고 남는 전하) 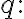
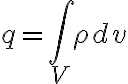
→ 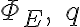 사이에는
사이에는
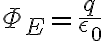 가 성립
가 성립
→ 이것을 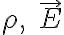 로 표현하면
로 표현하면
* 실제로는 쿨롱 법칙보다 가우스 법칙을 많이 씀
* 가우스 법칙 좌변의 적분은 가우스 표면에서 전기장 값을 먼저 알아야 구하는 게 가능
* 가우스 법칙으로 전기장을 구할 수는 없지만, 가우스 법칙 자체는 언제나 성립
* 전하 분포가 특별한 경우에만 (전하분포에 대칭성이 있을 때) 가우스 법칙을 써서 전기장을 구할 수 있음
* 가우스 법칙 좌변의 적분은 가우스 표면에서 전기장 값을 먼저 알아야 구하는 게 가능
* 가우스 법칙으로 전기장을 구할 수는 없지만, 가우스 법칙 자체는 언제나 성립
* 전하 분포가 특별한 경우에만 (전하분포에 대칭성이 있을 때) 가우스 법칙을 써서 전기장을 구할 수 있음
그리하여 가우스 법칙을 적용가능한 전하분포 패턴은 한정되어 있는데
- 점전하
- 무한히 긴 균일한 선전하
- 무한히 넓은 균일한 면전하
점전하가 만드는 전기장
점전하 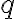 를 중심으로 하고, 반지름
를 중심으로 하고, 반지름  인 구의 표면을 가우스 폐곡면으로 정함.
인 구의 표면을 가우스 폐곡면으로 정함.
그러면 대칭성에 의해 구 표면 전기장의 세기는 모두 같고, 전기장 방향은 모두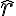 방향.
방향.
=E(r)\hat{r})
그래서, 법칙의 좌변: 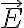 와
와 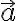 방향이 같으므로,
방향이 같으므로, 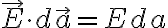 이므로
이므로
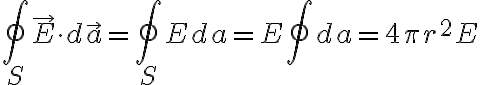
법칙의 우변:
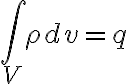
따라서
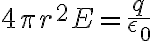
=\frac{1}{4\pi\epsilon_0}\frac{q}{r^2}\hat{r})
이 결과를 보면 쿨롱 법칙과 동일한 것을 알 수 있음
그러면 대칭성에 의해 구 표면 전기장의 세기는 모두 같고, 전기장 방향은 모두
무한히 긴 균일한 선전하가 만드는 전기장
가우스표면은 원통 모양,
선전하가 중심축에 있고,
원통 단면 반지름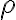 이고,
이고,
길이가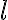 인 원통 표면을 가우스 폐곡면으로 정함
인 원통 표면을 가우스 폐곡면으로 정함
원통 표면에서는 전기장 세기가 모두 같고, 원통 표면 어디서나 전기장 방향은
선전하가 중심축에 있고,
원통 단면 반지름
길이가
원통 표면에서는 전기장 세기가 모두 같고, 원통 표면 어디서나 전기장 방향은
7. 가우스의 전기장 법칙 ¶
가정: 구형 도체
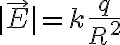 이고 공의 표면적
이고 공의 표면적 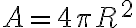 이므로
이므로
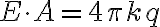
여기에

를 넣으면
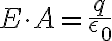
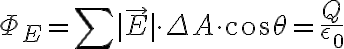
- 도체 내부의 전기장은 0이다. (표면에만 있다.)
- 도체 표면과 전기장선의 각도는 90°이다.
Q = 표면에 싸인 내부의 전하량
평행판 축전기,capacitor를 가정하면, (이렇게 해야 다음 내용이 말이 되는지?? CHK)
(그걸 가정하는 이유는 전기장이 판 사이에서 일정하다고 놓기 위한 것이 맞는지? CHK)
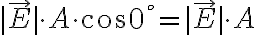
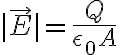
여기서 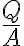 는 면전하밀도
는 면전하밀도 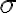 이므로 (전하밀도,charge_density)
이므로 (전하밀도,charge_density)
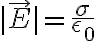
(그걸 가정하는 이유는 전기장이 판 사이에서 일정하다고 놓기 위한 것이 맞는지? CHK)
9. ysi ¶
먼저 전속,electric_flux(Ψ)은 전속밀도(D)에 대해
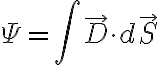 (임의의 면적에 대해)
(임의의 면적에 대해)
인데, 가우스법칙은
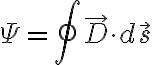 (폐곡면에 대해)
(폐곡면에 대해)
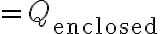 (Q는 그 폐곡면이 싸고 있는 전하량)
(Q는 그 폐곡면이 싸고 있는 전하량)
즉, 전하에서 발산해나오는 전속은 그 원인이 되는 전하량과 같다는 것.
가우스 법칙은 대칭성이 확보된 때만 적용한다.
가우스평면(가우스면, 가우시안 폐곡면)은 대칭성도 중요하고
다음 조건도...
가우스평면(가우스면, 가우시안 폐곡면)은 대칭성도 중요하고
다음 조건도...
접선 조건 :  (계산이 편해짐)
(계산이 편해짐)
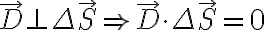
접선조건만으로 되면 충분하겠지만 안되면 법선조건도 써서.또한 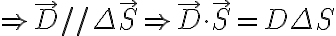
법선 조건: 가우스법칙 적용 예: y축 따라가는 무한직선, 선전하밀도 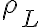
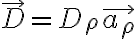 , 무엇의 함수냐면
, 무엇의 함수냐면
\vec{a_{\rho}}) 즉 rho만의 함수. (D는 phi, z에 관계없이 일정)
즉 rho만의 함수. (D는 phi, z에 관계없이 일정)
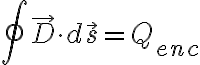
좌변 = 옆면적분 + 윗면적분 + 아랫면적분
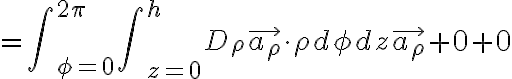
 (h))
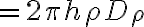
우변
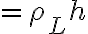
즉 h가 소거되고

구하는 것은
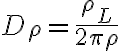
따라서
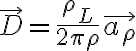 (C/m2)
(C/m2)
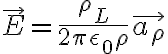 (V/m)
(V/m)
![[http]](/123/imgs/http.png) src 3강 1h:2m 2020-10-14
src 3강 1h:2m 2020-10-14
Next: see 발산,divergence#s-1(ysi)
좌변 = 옆면적분 + 윗면적분 + 아랫면적분
![[http]](/123/imgs/http.png) src 3강 1h:2m 2020-10-14
src 3강 1h:2m 2020-10-14Next: see 발산,divergence#s-1(ysi)

