1. 1 ¶
표기:
) 혹은
혹은 )
여기서
 : 시행 횟수, number of observation, 베르누이_시행,Bernoulli_trial의 반복 횟수, ... 양의 정수.
: 시행 횟수, number of observation, 베르누이_시행,Bernoulli_trial의 반복 횟수, ... 양의 정수.
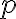 : 발생 확률(probability of occurrence), 각 시행의 성공 확률, ...
: 발생 확률(probability of occurrence), 각 시행의 성공 확률, ... ![$[0,1]$ $[0,1]$](/123/cgi-bin/mimetex.cgi?\Large [0,1]) 내의 실수.
내의 실수.
 :
:  번 시행 중 성공의 횟수
번 시행 중 성공의 횟수
성공 확률이 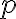 인 베르누이 시행을
인 베르누이 시행을  번 반복해서 성공횟수가 확률변수
번 반복해서 성공횟수가 확률변수  이면, X가 이항확률변수,binomial_random_variable이다.
이면, X가 이항확률변수,binomial_random_variable이다.
각 베르누이 시행은 서로 독립이다. (독립시행)
1회 시행마다 사건이 일어날 확률 p,
일어나지 않을 확률 (또는 여사건이 일어날 확률) q(=1-p)라 하고,
n회의 독립시행 중 사건이 일어나는 횟수가 X이면,
X는 0, 1, 2, …, n중 한 값을 가지는 확률변수이며,
X=x가 되는 확률은,
i.e.
X의 확률질량함수,probability_mass_function,PMF는
=\binom{n}{x}p^{x}q^{n-x})
(계수는 이항정리,binomial_theorem에 의해 계산할 수 있다.)
1회 시행마다 사건이 일어날 확률 p,
일어나지 않을 확률 (또는 여사건이 일어날 확률) q(=1-p)라 하고,
n회의 독립시행 중 사건이 일어나는 횟수가 X이면,
X는 0, 1, 2, …, n중 한 값을 가지는 확률변수이며,
X=x가 되는 확률은,
i.e.
X의 확률질량함수,probability_mass_function,PMF는
이런 분포를 이항분포라 하고, 기호로
)
로 나타낸다.
Ex. 주사위를 7번 던진다면
)
주사위를 4회 던져서 6이 2회 나올 확률:
^2\left(\frac{1}{6}\right)^2=\frac{25}{216})
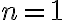 인 경우는 베르누이_분포,Bernoulli_distribution.
인 경우는 베르누이_분포,Bernoulli_distribution.
)
베르누이 분포는 이항분포의 특수한 경우이다. (시행 횟수가 한번인 경우)
베르누이 분포는 이항분포의 특수한 경우이다. (시행 횟수가 한번인 경우)
// ㄷㄱㄱ week 7-1 14m
Binomial Distribution
The number of successes among 𝑛 Bernoulli trails
• When transmission error probability is 0.1, probability to have 2 errors for 10 transmissions

 이 커질수록 bell shape로 감을 볼 수 있다
이 커질수록 bell shape로 감을 볼 수 있다
• When transmission error probability is 0.1, probability to have 2 errors for 10 transmissions
𝑝 = 0.19

베르누이_시행,Bernoulli_trial에서 한쪽 사건이 일어날 확률(성공확률이라고 하는 일이 많다)을 알고 있을 때 이 시행을  번 반복했을 때 그 사건이 일어나는 횟수(성공 횟수)는 이항분포를 따른다.
번 반복했을 때 그 사건이 일어나는 횟수(성공 횟수)는 이항분포를 따른다.
| 확률 |
이 확률분포를 성공확률 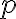 와 시행횟수
와 시행횟수  의 이항분포라고 하고
의 이항분포라고 하고
)
라는 기호로 나타낸다.
확률변수  가 이항분포
가 이항분포 ) 에 따를 때
에 따를 때  의 기대값,expected_value(평균,mean,average), 분산,variance, 표준편차,standard_deviation는
의 기대값,expected_value(평균,mean,average), 분산,variance, 표준편차,standard_deviation는
=np)
=np(1-p))
=\sqrt{np(1-p)})
(나가노 히로유키)
4. 이항확률변수,binomial_random_variable ¶
PMF:
=\binom{n}{x}p^xq^{n-x})
where
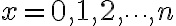
=np)
=npq)
A random experiment is repeated  independent times.
independent times.
Let be the number of times a certain event
be the number of times a certain event  occurs in
occurs in  trials.
trials.

(X be the binomial r.v. with parameter n and p)
![$P[X=k]=\binom{n}{k} p^k (1-p)^{n-k}$ $P[X=k]=\binom{n}{k} p^k (1-p)^{n-k}$](/123/cgi-bin/mimetex.cgi?\Large P[X=k]=\binom{n}{k} p^k (1-p)^{n-k})
성질:
![$\sum p[X=k]=1$ $\sum p[X=k]=1$](/123/cgi-bin/mimetex.cgi?\Large \sum p[X=k]=1)
![[https]](/123/imgs/https.png) 수학백과: 이항확률변수
수학백과: 이항확률변수
이산확률변수,discrete_random_variable와 관계?
Let
where
is the indication function for the event
in the
th trial
- Sample space
(X be the binomial r.v. with parameter n and p)
for 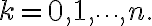
![[https]](/123/imgs/https.png) 수학백과: 이항확률변수
수학백과: 이항확률변수이산확률변수,discrete_random_variable와 관계?
}
6. Twins ¶
https://angeloyeo.github.io/2021/04/23/binomial_distribution.html
![[https]](/123/imgs/https.png) 수학백과: 이항분포
수학백과: 이항분포
https://everything2.com/title/binomial distribution
http://www.moonrepeat.org/wiki/doku.php?id=이항분포
![[https]](/123/imgs/https.png) 수학백과: 이항분포
수학백과: 이항분포https://everything2.com/title/binomial distribution
http://www.moonrepeat.org/wiki/doku.php?id=이항분포
Related:
베르누이_분포,Bernoulli_distribution는 이항분포에서 n이 1인 경우임.
이항분포는 결과가 2가지일 때. 다항분포,multinomial_distribution는 결과가 3가지 이상일 때.
푸아송_분포,Poisson_distribution:
 이항확률변수,binomial_RV
이항확률변수,binomial_RV
이항분포는 결과가 2가지일 때. 다항분포,multinomial_distribution는 결과가 3가지 이상일 때.
푸아송_분포,Poisson_distribution:
이항분포가 n이 크고 p가 0에 가까울 때, λ=np인 푸아송 분포로 근사 가능. { λ가 크다면 정규분포,normal_distribution로 근사 가능 }

