이것도? - yes.
^n=a_0+a_1(x-c)+a_2(x-c)^2+a_3(x-c)^3+\,\cdots)
여기서 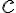 를 center라고 한다. (중심,center)
를 center라고 한다. (중심,center)
바로 위 멱급수는
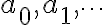 는 당연히 계수,coefficients.
는 당연히 계수,coefficients.
바로 위 멱급수는
- power series in
- power series centered at
- power series about
그러니까 무한차 다항식,polynomial? CHK
A power series about 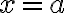 is a sum of constants times powers of
is a sum of constants times powers of ) :
:
+C_2(x-a)^2+\cdots+C_n(x-a)^n+\cdots=\sum_{n=0}^{\infty}C_n(x-a)^n)
수렴반경 : 특정 조건을 만족하는 실수 ...
수렴구간
정의.
x=0을 중심으로 하는 멱급수(power series about x=0):
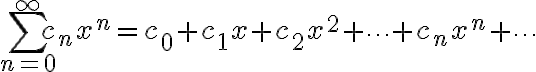
x=a를 중심으로 하는 멱급수(power series about x=a):
^n = c_0 + c_1(x-a) + c_2(x-a)^2 + \cdots + c_n(x-a)^n + \cdots)
여기서  는 중심,center, 상수,constant
는 중심,center, 상수,constant 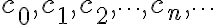 는 계수,coefficient라 한다.
는 계수,coefficient라 한다.
x=0을 중심으로 하는 멱급수(power series about x=0):
(Thomas 13e ko)
5. 멱급수의 수렴 반지름 ¶
멱급수 =\sum c_n x^n) 을 고려하자. 급수의 수렴 혹은 발산은 입력 변수
을 고려하자. 급수의 수렴 혹은 발산은 입력 변수  를 어떻게 선택하느냐에 따라 달라진다. 수렴 반지름은
를 어떻게 선택하느냐에 따라 달라진다. 수렴 반지름은 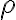 로 표기하는데, 이 값은 n제곱근 판정법 혹은 비율 판정법을 사용하여 구할 수 있다.
로 표기하는데, 이 값은 n제곱근 판정법 혹은 비율 판정법을 사용하여 구할 수 있다.
![$\frac{1}{\rho}=\lim_{n\to\infty}\sqrt[n]{|c_n|}=\lim_{n\to\infty}\left|\frac{c_{n+1}}{c_n}\right|$ $\frac{1}{\rho}=\lim_{n\to\infty}\sqrt[n]{|c_n|}=\lim_{n\to\infty}\left|\frac{c_{n+1}}{c_n}\right|$](/123/cgi-bin/mimetex.cgi?\Large \frac{1}{\rho}=\lim_{n\to\infty}\sqrt[n]{|c_n|}=\lim_{n\to\infty}\left|\frac{c_{n+1}}{c_n}\right|)
멱급수 =\sum_{n=0}^{\infty}c_n x^n) 은 모든
은 모든 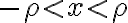 에 대해 수렴한다.
에 대해 수렴한다.
(Ivan Savov)
… 지금까지 공부한 것에 의하면 급수 ^n) 의 수렴에 대해 세 가지가 가능하다. 즉
의 수렴에 대해 세 가지가 가능하다. 즉 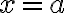 에서만 수렴하거나, 모든 점에서 수렴하거나,
에서만 수렴하거나, 모든 점에서 수렴하거나, 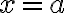 를 중심으로 반지름이
를 중심으로 반지름이 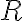 인 어떤 구간에서 수렴한다. …
인 어떤 구간에서 수렴한다. …
(위 '멱급수의 수렴정리'의 따름정리)
급수 ^n) 의 수렴성은 다음 세 가지 중의 하나이다.
의 수렴성은 다음 세 가지 중의 하나이다.
- 양수
이 존재하여
인 모든
에 대하여 발산하고 // 반지름,radius밖에선 발산,divergence
인 모든
에 대해 절대수렴한다. // 반지름 안에선 절대수렴,absolute_convergence
양 끝점인에서는 급수에 따라 수렴할 수도 있고 발산할 수도 있다.
- 모든
에 대해 절대수렴한다. -
인 경우
에서만 수렴하고 그 외 모든 점에서 발산한다 -
인 경우
(Thomas 13e ko)
8.2. p A50 ¶
멱급수 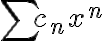 에 대해, 다음 세 가지 가능성밖에 없다. (다음 세 가지 중 하나이다?)
에 대해, 다음 세 가지 가능성밖에 없다. (다음 세 가지 중 하나이다?)
일 때만 수렴한다.
- 모든
에 대해 수렴한다.
이면 급수가 수렴하고,
이면 급수가 발산하는 그런 양수
이 존재한다.
멱급수 ^n) 에 대해 다음 세 가지 가능성밖에 없다.
에 대해 다음 세 가지 가능성밖에 없다.
일 때만 수렴한다.
- 모든
에 대해 수렴한다.
이면 급수가 수렴하고,
이면 급수가 발산하는, 그런 양수
이 존재한다.


![[https]](/123/imgs/https.png)
![[http]](/123/imgs/http.png)