t를 시간, C를 시간 t에서의 물체의 궤적,
=(x(t),y(t),z(t)))
t=a일 때의 시점(initial point),y(a),z(a)))
t=b일 때의 종점(terminal point),y(b),z(b)))
시점과 종점이 같은 경우 closed
이렇게 생각할 수 있음
(continuous, differentiable, simple, smooth는 생략 - 책 참조)
t=a일 때의 시점(initial point)
t=b일 때의 종점(terminal point)
시점과 종점이 같은 경우 closed
이렇게 생각할 수 있음
(continuous, differentiable, simple, smooth는 생략 - 책 참조)
나중에 TBW
(O'Neil 7e 12.1 p367)
책 앞 line integral 표기법 안내:
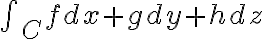
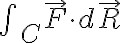 위와 마찬가지.
위와 마찬가지. 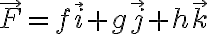 일 때.
일 때.
ds) line integral of
line integral of  over
over 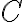 w.r.t. arc_length
w.r.t. arc_length
z축이 ) 인 그래프를 그리고 설명함
인 그래프를 그리고 설명함
)
)

2차원 평면에서 arc_length(curr goto 호,arc)의 매우 작은 변화 (미분,differential) ds는
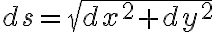 (피타고라스 정리)
(피타고라스 정리)
구하는 것은
ds) (이하 t=a에서 t=b 까지 가는 것을 곡선 C?라고 표시)
(이하 t=a에서 t=b 까지 가는 것을 곡선 C?라고 표시)
,y(t))\sqrt{dx^2+dy^2})
이것을 t에 대해 나타내야 하므로
,y(t))\sqrt{(\frac{dx}{dt})^2+(\frac{dy}{dt})^2}dt)
위 조건에서 ,\,dy/dt=h%27(t)) ...
...
from Khan: Introduction to the line integral https://youtu.be/_60sKaoRmhU
벡터장,vector_field 안에서만 의미가 있나?
벡터장 A, 곡선 L이 주어질 때, L위의 점 a에서 b까지 움직이면서 미소길이(접선,tangent_line방향의 매우 짧은 벡터, 접벡터,tangent_vector 인지 CHK)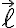 이 받는 A의 영향은 스칼라곱,scalar_product,dot_product
이 받는 A의 영향은 스칼라곱,scalar_product,dot_product
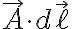
이고 이것을 선적분하면 (두번째 식은 개곡선일때만)
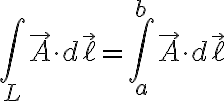
이고 폐경로일땐(원래 자리로 돌아옴, 즉 a→b→a→b..., 순환circulation)
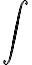 대신
대신 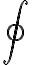
를 씀?
벡터장 A, 곡선 L이 주어질 때, L위의 점 a에서 b까지 움직이면서 미소길이(접선,tangent_line방향의 매우 짧은 벡터, 접벡터,tangent_vector 인지 CHK)
from https://www.youtube.com/watch?v=r4okf9RAVWo ; CHK
Related: 보존력,conservative_force개념과 깊은 연관이 있는듯?
알짜힘이 다음과 같으므로
)\cdot r%27(t))
a에서 b까지 받은 바람의 영향의 총합은
)\cdot r^{\prime}(t)dt)
여기서
=\frac{dr(t)}{dt})
=r^{\prime}(t) dt)
이므로 적분식은
\cdot dr)
이 된다
scalar field에서는
vector field에서는
W = F · s 와 관련이 깊다.
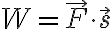
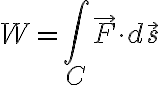
↓
2020-09-18
line 대신 curve 라고도 하나보다 (이게 더 옳지 않나? line은 보통 직선 뉘앙스 아닌가)
선적분 curve integral https://pinkwink.kr/215
line 대신 curve 라고도 하나보다 (이게 더 옳지 않나? line은 보통 직선 뉘앙스 아닌가)
선적분 curve integral https://pinkwink.kr/215
선적분
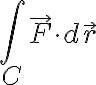
에서
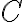 : 적분할 경로
: 적분할 경로
) : 피적분함수
: 피적분함수
특히 적분할 경로가 폐곡선인 경우, 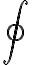 기호를 쓰며, 값을
기호를 쓰며, 값을 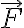 의
의 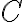 에 대한 circulation이라고 부름
에 대한 circulation이라고 부름
2020-09-16 from https://www.youtube.com/watch?v=Sa7xDuWEvZ4 스토크스 정리와 다이버젠스 정리 5:30 (차동우)

