기호 |…|
2. 성질 ¶
증명 팁:
iff
iff
iff
or
3. Geometric interpretations ¶
x와 c 사이 거리가 d이다.
x와 c 사이 거리가 d보다 크다.
x와 c 사이 거리가 d보다 작다.
x와 c 사이 거리가 d보다 작고, x≠c 이다.
거리,distance원점,origin에서의 거리 = 절대값?
실직선real_number_line(curr. 실수,real_number), 복소평면,complex_plane에서는 확실. tbw: 확장되면? ex. 사원수,quaternion라던지
두 수의 차의 절대값은 거리와 밀접한데 구체적으로 tbw.두 실수,real_number의 차이,difference의 절대값은 real_line 위에서 두 실수 사이의 거리,distance로 해석 가능 - ? 내생각, chk
차원이 높아져서 벡터의 뺄셈,subtraction의 절대값은 어떤지... chk, 그냥 단순 확장은 아닌듯, 일단 2d평면 위의 거리의 경우만 보면 제곱-합-제곱근이 들어가서... 이건 노름,norm관련이고...
이 사실들은 극한,limit의 엄밀한 정의(극한_EpsilonDeltaLimitDefinition)를 하는데 쓰인다.5. 자연스러운 절대값과 그게 아닌 것 ¶
https://horizon.kias.re.kr/13825/
p진수,p-adic_number 관련 시리즈 첫번째 글인데 중간 쯤 「‘절대값’이란?」 참조
저기선, 자연스러운 절대값:
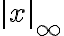
p진 절대값:
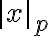
으로 표기.
5 공리를 만족하면 아르키메데스 절대값archimedean absolute value
그렇지 않은 비非아르키메데스 절대값non-archimedean absolute value
소수 p에 대해 정의할 수 있는 p진 절대값p-adic absolute value
p진수,p-adic_number 관련 시리즈 첫번째 글인데 중간 쯤 「‘절대값’이란?」 참조
저기선, 자연스러운 절대값:
5 공리를 만족하면 아르키메데스 절대값archimedean absolute value
그렇지 않은 비非아르키메데스 절대값non-archimedean absolute value
소수 p에 대해 정의할 수 있는 p진 절대값p-adic absolute value
6. 복소수 ¶
// 복소수의 절대값. rel. 복소해석,complex_analysis
복소수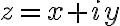
그것의 켤레(켤레복소수,complex_conjugate)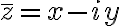
해당하는 극좌표) 즉
즉

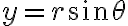
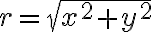
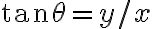
일 때 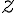 의 절대값( modulus or the absolute value of
의 절대값( modulus or the absolute value of 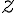 )은
)은
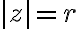
이며
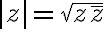
로 계산할 수도 있다. 그리고 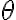 는 argument or amplitude of
는 argument or amplitude of 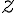 이며
이며
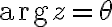
로 쓴다.
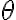 에
에  의 정수배가 더해져도
의 정수배가 더해져도 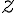 가 동일한데,
가 동일한데, 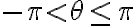 인 경우를
인 경우를 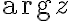 의 주치,principal_value라 하며
의 주치,principal_value라 하며 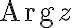 로 쓴다.
로 쓴다.
(Chan Man Advanced Math)
복소수
그것의 켤레(켤레복소수,complex_conjugate)
해당하는 극좌표
(Chan Man Advanced Math)
행렬식 ≠ 절대값 (주의)
예를 들어
(Zill 6e ko 8.4 행렬식 p489)
(주의: 순서론order_theory의 주제 순서,order와는 다름. 오히려 집합론,set_theory의 cardinality에 더 가까운?)
Twins:
https://planetmath.org/orderofagroup
https://mathworld.wolfram.com/GroupOrder.html
https://groupprops.subwiki.org/wiki/Order_of_a_group
https://ncatlab.org/nlab/show/order of a group
.... 그리고 https://encyclopediaofmath.org/wiki/Order 이건 매우 여러가지를 한번에 설명하는 페이지. 참고용. }
집합,set의 cardinality(writing)의
기호는 여러가지인데 n(A), |A|, #A, card(A) ... 마지막 것이 제일 명확한데.
저것은 번역어도 중구난방: {크기, 개수, 농도, ...}
아무튼 |...| 기호는 다양하게 쓰인다. Q1. 혹시 절대값이 먼저인지? Q2. 그렇다면 저 기호를 채택한 이유가 절대값과 어떤 유사성이 있기 때문? or not?저것은 번역어도 중구난방: {크기, 개수, 농도, ...}
... 이상 이것들 mv to 표기법,notation?
기타
algebraic_number_theory에선 absolute_norm , absolute_trace 도 정의한다..... chkout: https://planetmath.org/normandtraceofalgebraicnumber
algebraic_number_theory에선 absolute_norm , absolute_trace 도 정의한다..... chkout: https://planetmath.org/normandtraceofalgebraicnumber
표준어: 절댓값
https://encyclopediaofmath.org/wiki/Absolute_value - modulus, of a real number  (다른 EoM 항목보다 훨씬 easy)
(다른 EoM 항목보다 훨씬 easy)
https://planetmath.org/AbsoluteValue
https://mathworld.wolfram.com/AbsoluteValue.html
 Absolute_value
Absolute_value
 절댓값
절댓값
https://artofproblemsolving.com/wiki/index.php/Absolute_value (del ok)
https://planetmath.org/AbsoluteValue
https://mathworld.wolfram.com/AbsoluteValue.html
https://artofproblemsolving.com/wiki/index.php/Absolute_value (del ok)
https://ncatlab.org/nlab/show/absolute value
http://oeis.org/wiki/Absolute_value
{
실수인 경우는 명백하고, 복소수,complex_number 관련해 Complex norm에서 complex_norm(노름,norm?) complex_modulus(법,modulus?) 둘은 같은? - 을 언급
}
http://oeis.org/wiki/Absolute_value
{
실수인 경우는 명백하고, 복소수,complex_number 관련해 Complex norm에서 complex_norm(노름,norm?) complex_modulus(법,modulus?) 둘은 같은? - 을 언급
}
----
- [1]
 Absolute_value 첫 문장 "the absolute value or modulus of a real number x, denoted |x|, …"
Absolute_value 첫 문장 "the absolute value or modulus of a real number x, denoted |x|, …"

