기대값,expected_value

pagename to 'expectation'? or 기대,expectation라는 페이지를 만들?

AKA 기댓값(표준어), 기대치, expected value, expectation value, EV, expectation
AKA first moment, mean, average (see 모멘트,moment, 평균,mean,average)

expectation과 mean의 차이 => https://blog.naver.com/sw4r/221010499304

// from https://suhak.tistory.com/938
{
(이산확률변수,discrete_random_variable X) 확률질량함수,probability_mass_function,PMF $f$ 일 때

$E(X)=\sum_x xf(x)$

(연속확률변수,continuous_random_variable X) 확률밀도함수,probability_density_function,PDF $f$ 일 때

$E(X)=\int_{-\infty}^{\infty}xf(x)dx$

}

// ㄷㄱㄱ
Expectation: a fixed value that represents the value of a random variable.
Discrete RV의 경우:

$\text{E}[X]=\mu_X=\sum_{x\in S_X} x P_X (x)$

Continuous RV의 경우:

$\text{E}[X]=\mu_X=\int_{-\infty}^{\infty} xf_X(x)dx$

Ex. rolling a dice

1 × 1/6 + 2 × 1/6 + … + 6 × 1/6 = 3.5

표본평균,sample_mean은 기대값과 다르다. 기대값은 고정된 값이며 표본평균은 무작위에 의존한다.
표본평균은 실험(see 확률실험,random_experiment and 시행,trial)을 많이 할 수록(더 많은 표본,sample이 있을수록) 기대값에 가까워진다 → 큰 수의 법칙 law of large numbers ...

큰수의법칙

Sub:
expectation_maximization
{
번역?
기대값최대화 ?

Sub:
기대값최대화 알고리듬 expectation-maximization algorithm
expectation-maximization_algorithm = EM algorithm

MKLINK: 반복,iteration 알고리듬,algorithm 최대가능도,maximum_likelihood maximum_a_posteriori(MAP, 최대사후확률)

기댓값_최대화_알고리즘

Expectation–maximization_algorithm
...

expectation-maximization algorithm

Up: 기대값,expected_value(or expectation) 최대화,maximization
}

모평균,population_mean, 기호 μ

$E(X)$ 는 기대값에서 온 기호인가? 평균으로 많이 언급되는데..

{
성질

$E(aX)=aE(X)$
$E(b)=b$
$E(aX+b)=aE(X)+b$

}

이산형일 경우

$\bar{x}=\frac{x_1n_1+x_2n_2+\cdots+x_kn_k}{n}$

$=x_1\cdot\frac{n_1}{n}+x_2\cdot\frac{n_2}{n}+\cdots+x_k\cdot\frac{n_k}{n}$
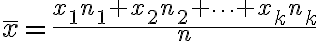
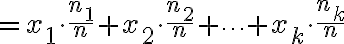
$=x_1P(X=x_1)+x_2P(X=x_2)+\cdots+x_kP(X=x_k)$
$=x_1f(x_1)+x_2f(x_2)+\cdots+x_kf(x_k)$
$=\sum x_if(x_i)$

연속형일 경우

$\int xf(x)dx$

i.e.

$\bar{x}=\frac{x_1n_1+x_2n_2+\cdots+x_kn_k}{n}=\sum x_i\frac{n_i}{n} = \sum x_i p_i$

$p_i={n_i}/n$ 은 확률,probability

Contents

1. 확률변수 X의 기대값 또는 평균

2. 이산형분포의 기대값

3. 연속형분포의 기대값

4. 조건부 기대값 conditional expected value

5. 정리: X, Y가 독립일때 X×Y의 기대값

6.1. 기대값

6.2. 결합확률분포에 대한 기대값

6.3. 확률변수가 함수 형태로 주어지는 경우

6.3.1. ex. g(X,Y)=X+Y의 기대값 구하기
6.3.2. ex. g(X,Y)=aX+b의 기대값 구하기
6.3.3. ex. X와 Y 가 독립일 때, g(X,Y)=XY의 기대값 구하기

6.4. summary

8. 분산과의 관계

9. 표본평균과의 관계

1. 확률변수 X의 기대값 또는 평균 ¶

확률변수,random_variable의 기대값 또는 평균,mean,average
$E(X)=\sum_{i=1}^{n}x_ip_i=x_1p_1+x_2p_2+\cdots+x_np_n$

확률분포,probability_distribution가 이산형인지 연속형인지에 따라 구분.

//tmp from 서울과기대 http://www.kocw.net/home/search/kemView.do?kemId=1162312 4장_확률변수와분포_기대값

2. 이산형분포의 기대값 ¶

X의 기대값:

$E(X)=\sum_{x\in R}xf(x)$

여기서

X: 확률변수
R: 확률변수 X의 치역,range
f: 확률함수 (이산형)

이산확률변수,discrete_random_variable $X$ 에 대한 기대값 $E[X]$ 는 다음과 같이 계산.

$E{[X]=\sum_{x\in S} xP(X=x)$

(단, $S$ 는 표본공간,sample_space)

3. 연속형분포의 기대값 ¶

X의 기대값(평균): 적분

$\int_{-\infty}^{\infty}|x|f(x)dx$

가 존재할 때 $X$ 의 기대값

$E(X)=\int_{-\infty}^{\infty}xf(x)dx$

이 존재한다.
여기서

f: 확률변수 X의 확률밀도함수,probability_density_function,PDF

4. 조건부 기대값 conditional expected value ¶

Moved to 조건부기대값,conditional_expected_value

5. 정리: X, Y가 독립일때 X×Y의 기대값 ¶

두 확률변수 X, Y가 독립이면

$E(X\times Y)=E(X)\times E(Y)$

6. tmp ¶

from http://blog.naver.com/mykepzzang/220837877074

6.1. 기대값 ¶

확률변수 X의 확률분포함수가 $f(x)$ 일 때 X의 기대값 E(X)는
이산확률변수,discrete_random_variable일 경우

$E(X)=\sum_x x\cdot f(x)$

연속확률변수,continuous_random_variable일 경우

$E(X)=\int_{-\infty}^{\infty}x\cdot f(x)dx$

6.2. 결합확률분포에 대한 기대값 ¶

확률변수 X, Y의 결합확률분포함수가 $f(x,y)$ 일 때 (see 결합확률분포,joint_probability_distribution)
이산확률변수의 경우

$\mu_x=E(X)=\sum_x x\cdot f_X(x)$
$\mu_y=E(Y)=\sum_y y\cdot f_Y(y)$

연속확률변수의 경우

$\mu_x=E(X)=\int_{-\infty}^{\infty}x\cdot f_X(x)dx$
$\mu_y=E(Y)=\int_{-\infty}^{\infty}y\cdot f_Y(x)dy$ ..... $(y)$ 아닌가?

여기서 $f_X(x),f_Y(x)$ 는 주변확률분포 .... $f_Y(y)$ 아닌가?

6.3. 확률변수가 함수 형태로 주어지는 경우 ¶

확률변수 X와 Y의 결합확률함수가 $f(x,y)$ 일 때, 확률변수 $g(X,Y)$ 의 기대값은
이산확률변수의 경우

$\mu_{g(X,Y)}=E(g(X,Y))=\sum_x \sum_y g(x,y)\cdot f(x,y)$

연속확률변수의 경우

$\mu_{g(X,Y)}=E(g(X,Y))=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}g(x,y)\cdot f(x,y) dxdy$

6.3.1. ex. g(X,Y)=X+Y의 기대값 구하기 ¶

(이하 $\int_{-\infty}^{\infty}\;\to\;\int$ 로 표기)

$E(X+Y)=\iint (x+y)f(x,y)dxdy$

$=\iint xf(x,y)+yf(x,y)dxdy$
$=\iint xf(x,y)dxdy+\iint yf(x,y)dxdy$
$=E(X)+E(Y)$

6.3.2. ex. g(X,Y)=aX+b의 기대값 구하기 ¶

$E(aX+b)=\int(ax+b)f(x)dx$

$=\int ax f(x)+bf(x) dx$
$=\int axf(x)dx+\int bf(x)dx$
$=a\int xf(x)dx+b\int f(x)dx$
$=aE(X)+b$

즉 기대값의 선형성,linearity이 성립.

6.3.3. ex. X와 Y 가 독립일 때, g(X,Y)=XY의 기대값 구하기 ¶

$E(XY)=\iint xyf(x,y)dxdy$

$=\iint xyf_X(x)f_Y(y)dxdy$
$=\int xf_X(x)dx\cdot \int yf_Y(y)dy$
$=E(X)E(Y)$

여기서 $f_X(x),f_Y(x)$ 는 주변확률분포. .... $f_Y(y)$ 아닌가?

6.4. summary ¶

$E(X+Y)=E(X)+E(Y)$
$E(XY)=E(X)\cdot E(Y)$
$E(aX+b)=aE(X)+b$
$E(aX^2+bX+c)=aE(X^2)+bE(X)+c$
$E(aX+bY)=aE(X)+bE(Y)$

7. 한계 ¶

기대값은 분포의 중심 위치에 대한 정보를 주며, 흩어진 정도를 판별하는데는 도움이 되지 않는다. 흩어지거나 밀집된 정도를 파악하려면 산포도,dispersion가 필요하다.

8. 분산과의 관계 ¶

$(X-\mu)^2$ 의 기대값은 분산,variance이다.
따라서 (분산)≥0 이다.

9. 표본평균과의 관계 ¶

표본평균,sample_mean: an average of random samples from repeated experiments.
표본평균은 실험을 많이 할 수록 기대값에 가깝게 된다. - law_of_large_numbers

Related, Similar:

평균,mean,average

tmp; 평균값과 기대값은 같은가? 다르다고 함. 평균은 이미 일어난 것에 대한 것이고 기대값은 예측 개념을 포함하는 듯? from https://kagnouystudy.blogspot.com/2018/08/blog-post.html

대표값,평균값,중앙값,최빈값,
중심성향,central_tendency(from [1])(?), 무게중심(??)
적률,moment > 일차적률

Twins:

보면 모평균,population_mean과 매우 밀접, 정확한 src찾아 기술/mkl

Expected_value
https://mathworld.wolfram.com/ExpectationValue.html
[https]

[https]

수학백과: 기댓값
https://everything2.com/title/expectation
http://mlwiki.org/index.php/Expected_Value

Up: 통계,statistics

----

[1] https://terms.naver.com/entry.nhn?docId=3404994&ref=y&cid=47324&categoryId=47324