TODO MKCLEAR "functional space" 라는 표현이 있는데 확실히 disambig.

functional space functional space difference

function_space

functional_space

//tmp from wpen
두 고정된 집합 사이의 함수들의 집합.
...article에 있는 수식만 써보면

$(f+g)(x)=f(x)+g(x)$
$(c\cdot f)(x)=c\cdot f(x)$

(compare 선형성,linearity)

1. tmp 1 CHK
2. Bmks ko
3. TBW 벡터공간과의 비교

[edit]

1. tmp 1 CHK ¶

//tmp from https://m.blog.naver.com/spin898/221144108938
//글제목 Dot product(2) - function space

(벡터,vector - 함수,function)의 대칭성,symmetry 관계를 언급.

벡터,vector와 함수,function의 {크기, 내적, 직교} 조건을 비교하면

내적 // 스칼라곱,scalar_product,dot_product 내적,inner_product
벡터의 내적

$\vec{A}\cdot\vec{B}=\sum_{i=1}^{n}A_iB_i$

함수의 내적 // *는 conjugate.

$\langle A|B \rangle = \int_a^b A^{*}(x)B(x)dx$

크기 // 측도,measure? 노름,norm?
벡터의 크기

$\left| \vec{A} \right| = \sqrt{\sum_{i=1}^{n}A_i^2}$

함수의 크기 // dx빠진듯.....

$|A(x)|=\sqrt{\langle A|A \rangle}=\sqrt{\int_a^b A^*(x)A(x)}$

직교조건 // 직교성,orthogonality
벡터의 직교조건

$\vec{A}\cdot\vec{B}=0$

함수의 직교조건

$\langle A|B \rangle=0$

이상 세가지를 보면 symmetric하다고.. (see 대칭성,symmetry)

브라켓표기법,bra-ket_notation

$\langle A| = \int_a^b A^*(x)[\quad\quad]dx$
$|B\rangle = \begin{bmatrix}B_1\\B_2\\B_3\\\vdots\end{bmatrix}$

$A\cdot$ <- 이것 자체가 일종의 연산자,operator

bra를 이렇게 표현 가능

$\langle A| = \begin{bmatrix} A_1^* & A_2^* & A_3^* & \cdots\end{bmatrix}$

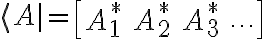
함수의 직교 조건. 구간 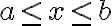$a\le x\le b$ 에서 다음을 만족하는 경우 두 함수 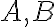$A,B$ 는 직교.

$\langle A|B\rangle=\int_a^b A^*(x)B(x)dx=0$

이하 이런것들 차례로 언급
그람-슈미트_과정,Gram-Schmidt_process,
완전성,completeness을 갖추기 위한 함수(벡터)들의 집합의 조건, // 혹시 완비성,completeness?
론스키언,Wronskian - 함수들의 집합이 선형독립,linear_independence인지 판단하는 방법,
내적공간,inner_product_space과 내적공간에 존재하는 서로 독립적이며 서로 내적이 0인 함수들인
직교함수,orthogonal_function(curr at 직교성,orthogonality). 함수공간에서는
코시-슈바르츠_부등식,Cauchy-Schwartz_inequality 또한 그대로 성립.

$\left|\int_a^b A^*(x)B(x)dx\right|^2\le \left(\int_a^b A^*(x)A(x)dx\right) \left(\int_a^b B^*(x)B(x)dx\right)$

파동함수,wave_function는 슈뢰딩거_방정식,Schroedinger_equation의 해,solution이며 무한차원을 가질 수 있고 무한차원 유클리드_공간,Euclidean_space은 힐베르트_공간,Hilbert_space이고 이건 완전한 내적공간....
슈뢰딩거방정식의 "일반적인 형태의 해"는
무한차원공간에 표현된 "임의의 벡터"와 같은 의미

[edit]

2. Bmks ko ¶

위상수학에서의 함수공간 https://freshrimpsushi.github.io/posts/function-space/
여러가지 함수공간 https://freshrimpsushi.github.io/posts/various-function-space/

[edit]

3. TBW 벡터공간과의 비교 ¶

벡터공간,vector_space과 유사.
//tmp from https://youtu.be/tZIcpm1-E1w?si=616TtDrif-7mcAIf&t=876
벡터

$\vec{v}=\sum_{i=1}^{\infty}v_i\hat{e_i}$
$\vec{v}=\sum_{i=1}^{\infty}\underbrace{v_i}_{\uparrow\atop{\rm component}}\underbrace{\hat{e_i}}_{\uparrow\atop\text{basis}}$

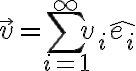
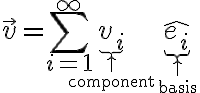
함수

$F(x)=\sum_{i=1}^{\infty}c_i f_i(x)$
$F(x)=\sum_{i=1}^{\infty}\underbrace{c_i}_{\uparrow\atop\text{coefficient}}\underbrace{f_i(x)}_{\uparrow\atop\text{basis}}$

규격화,normalization { "(틀)맞춤, 규격화" via

normalization }:

$\int_0^a f_i(x) f_j(x) dx = \delta_{ij}\begin{cases}N,&\text{if }\,i=j\\0,&\text{if }\,i\ne j\end{cases}$ 인 경우 scaling factor를 써서 $f(x)\to\frac1{\sqrt{N}}f(x)$ 로 치환하는 것: "basis를 normalization하기"

Twin:

수학의 세계: 함수공간

함수_공간

Vector_space#Function_spaces

Function_space
https://mathworld.wolfram.com/FunctionSpace.html
https://planetmath.org/functionspace

의 notation 목록 (많음) 보면 연속성,continuity/매끄러움,smoothness/...-rel 기호 C^뭐뭐 이것들이랑 적분가능성,integrability-rel 기호 L^뭐뭐(이건 아마 0/1/2/p/∞ 가 나오는 걸 보니 rel. metric, 노름,norm 의 L-뭐뭐 관련인데, chk and 정확한 관계 tbw) 이것들 등등 기호 정리 있음

Function_space

Up: 함수,function 공간,space topological_vector_space ( 벡터공간,vector_space and 위상공간,topological_space?? ) 선형대수,linear_algebra? 함수해석,functional_analysis?

VeryGoodWiki

This wiki is very good.
Minus sign: −

함수공간,function_space

Contents

1. tmp 1 CHK ¶

2. Bmks ko ¶

3. TBW 벡터공간과의 비교 ¶