통계,statistics

[edit]

통계학의 종류

TBW: descriptive vs inferential / bayesian vs frequentist / ...

기술통계학,descriptive_statistics - 자료의 정리 & 요약
주어진 자료의 특성을 분석.
추론통계학,inferential_statistics - 정보 분석으로 모집단의 특성을 추정/추론
주어진 자료를 이용하여 모집단,population의 특성을 추론.

tmp; 주로 추론,inference > 통계추론 or 통계적추론,statistical_inference 방식 접근(approach) 관점에서 나뉘는??? chk
Google:bayesian_statistics vs Google:frequentist_statistics ??
Google:bayesian frequentist

확률,probability
확률변수,random_variable
모집단,population: 통계적 관찰의 대상이 되는 집단 전체
전수조사(census): 모집단,population 전체를 대상으로 조사하는 것
추정하다(to estimate)라는 뜻의 라틴어 censere에서 유래
매우 힘들므로 보통 표본,sample을 뽑아 일부를 조사함
표본,sample: 모집단에서 뽑은 것
표본공간,sample_space: 랜덤 현상의 모든 가능한 결과,outcome의 집합
사건,event: 표본공간의 부분집합,subset
표본추출,sampling // Ndict:sampling Ndict:표본추출 Ndict:표집
{
표본추출, 표집, 샘플링

모집단,population으로부터 표본을 선택하는 행위
(같은 영단어 샘플링,sampling페이지는 전자공학 얘기)

복원추출(sampling with replacement) (추출할 때 마다 원래 상태로 돌려놓음)
비복원추출(sampling without replacement)

임의추출(random sampling; 확률적 추출) 무작위 추출 random_sampling
비임의추출(nonrandom sampling; 비확률적 추출)

표본추출오차(sampling error) = 통계량(statistic) - 모수(parameter) ...

// (노부호 p9-12)
{
표본오차(sampling error)란 모집단의 일부인 표본의 결과를 근거로 모집단 전체의 특성을 추론하는 과정에서 발생하는 오차를 말한다. 따라서 전수조사의 경우 표본오차는 발생하지 않는다. 표본오차는 일반적으로 표본의 크기가 증가함에 따라 감소한다.

표본추출 방법
  • 판단 표본추출(judgement sampling) - 전문가가 주관적으로 하는 샘플링
  • 확률 표본추출(probability sampling) - 표본 추출 전, 모집단을 구성하는 기본단위가 표본으로 추출될 확률을 일정하게 할당하는 방법, 판단표본추출보다 객관적
    • 단순 무작위 표본추출(simple random sampling) - 일정 크기의 모든 표본조합(sample combination)이 표본으로 추출될 확률을 같게 놓으며, 모집단의 기본단위가 표본에 포함될 확률을 같게 하여 표본추출하는 방법 - 이것의 무작위성,randomness을 확실히 하기 위해서는 난수발생기RNG를 사용 (일반적으로 난수,random_number는 고른분포,uniform_distribution로부터 만든 숫자로, 각 숫자가 발생할 확률은 동일)
    • 층화 표본추출(stratified sampling) - 각 층,stratum(writing) { 몇 개의 동질적인 집단으로 모집단,population을 구분해 놓은 것. (노부호 p11) } 에 가중값,weight을 적용하여 모집단 특성에 대한 추정치를 계산하는 방법
    • 군집 표본추출(clustered sampling) - 모집단을 군(cluster)으로 불리는 여러 집단으로 나누어 모집단을 대표하는 군을 표본으로 추출하는 방법
      • 1단계추출(single-stage sampling)
      • 2단계추출(two-stage sampling)
      • 다단계추출(multi-stage sampling)
    • 체계적 표본추출(systematic sampling) - 표본추출간격(sampling interval)(rel. 구간,interval)을 이용 - (대충) 그래서 (등차수열 비슷한 방식으로) 일정 간격으로 일부를 뽑아내는 - 다만 모집단의 순서,order에 따른 주기성,periodicity이 표본추출간격과 일치하는 경우 문제 발생
}

}


오차,error
자료,data
표본,sample
샘플링,sampling? - 통계에선 표본추출, 표집

사분위수,quartile
사분범위,interquartile_range,IQR
거리,distance
빈도,frequency
도수=빈도수=frequency: 각 계급,class에 들어가는 데이터의 수
상대도수: 도수의 합계에 대한 각 계급 도수의 비율 - see 빈도,frequency
누적상대도수: 그 계급 이하의 상대도수의 합계
기대값,expected_value




}

모수,parameter
모집단,population의 특성을 나타내는 수치.
모집단의 특성을 수치로 나타낸 것.
B(n, p)에서 n과 p
평균,mean,average, 분산,variance, 표준편차,standard_deviation, 분위수(사분위수,quartile, 백분위수,percentile), 모비율 등
[https]수학백과: 모수
모집단 전체 데이터를 얻을 수 없다면, 모집단의 특성을 나타내는 모수를 파악하여 모집단의 특성을 파악해볼 수 있다.

모집단,population의 특성을 수치로 나타낸 것 모수,parameter 모평균 μ나 모분산 σ2 등
표본,sample의 특성을 수치로 나타낸 것 통계량,statistic 표본평균 $\bar{X}$ , 표본분산 S2 등
모집단은 유일하게 존재, 표본은 여러 개 존재.


// from Ross p.20
표본평균(sample mean) - See 평균,mean,average
{
$\bar{x}=\sum_{i=1}^{n}\frac{x_i}{n}$
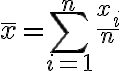
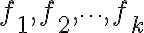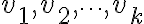빈도 $f_1, f_2, \cdots, f_k$ 를 갖는 $k$ 개의 서로 다른 값 $v_1, v_2, \cdots, v_k$ 에 대한 표본평균은 가중평균(weighted average)
$\bar{x}=\sum_{i=1}^{k}\frac{v_if_i}{n}$
}
// from Ross p.22
표본중앙값(sample median): 크기 n인 데이터 집합을 작은 것부터 나열하여서,
n이 홀수일 때 (n+1)/2 위치의 값
n이 짝수일 때 n/2 위치의 값과 n/2+1 위치의 값의 평균
// from Ross p.23
표본최빈값(sample mode): 가장 높은 빈도로 발생하는 값
최빈값들(modal values): 가장 높은 빈도로 발생하는 모든 값들 (단일값이 존재하지 않을 때)
표본분산,sample_variance
$s^2=\sum_{i=1}^{n}\frac{(x_i-\bar{x})^2}{n-1}$

표본평균과 표본분산 - 표본 페이지로..
{
$n$ 개의 표본,sample에서
표본평균,sample_mean
$\bar{X}=\frac1n\sum_{i=1}^n X_i$
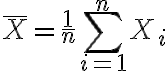
표본분산,sample_variance
$s^2=\frac1{n-1}\sum_{i=1}^n (X_i - \bar{X})^2$

이것들은 모집단,population의 특성인 모평균,population_mean과 모분산,population_variance을 추정할 때 쓰임.
}

계급,class
{
계급: 자료,data를 몇 개의 동등한 폭으로 나눈 구간,interval
계급값: 각 계급의 중앙값
몇 개의 계급을 나누어 도수분포표를 만듦
그룹의 개수를 구하는 방법은 여러가지가 있는데,
n=전체 자료의 수, k=그룹의 수라 할 때,
제곱근 방법 $k=\lceil\sqrt{n}\rceil$
Sturges 공식 $k=\lceil\log_2n+1\rceil$
Rice 공식 $k=\lceil2n^{1/3}\rceil$
화면이 흐려 ceil기호인지 확실하지 않음, CHK
// from Ross
값들을 여러 개의 그룹, 즉 계급구간(class interval)로 나누고 각 계급구간에 속하는 값의 개수를 표기.
계급구간의 양 끝점들을 계급경계(class boundary)라 함.
계급 데이터에 대한 막대그래프는 히스토그램,histogram.

같은 영단어: CS에서 class는 클래스,class.
}

누적빈도(또는 누적상대빈도)
누적빈도그래프,ogive
{
오자이브
}


(이하 plot/diagram/그래프,graph)
도수분포표,frequency_table
{
자료를 계급,class으로 나누고 각 계급의 도수(빈도수 frequency)를 조사하여 분포 상태를 나타낸 표.

Up: 표,table / 도수분포표는 변량이 1개일 때. 2개 이상이면 밑 참조
}
분할표,contingency_table, 교차표,cross_tabulation
{ Up: 표,table / 2개 이상의 변수에 대해 교차시켜 빈도를 표시한 표 }
산점도,scatter_plot scatterplot
{
$(x_1,\,y_1),\,\cdots,\,(x_n,\,y_n)$ 을 2차원 평면에 그림
}
산점도 행렬 scatter_matrix
시계열그림 time series plot - 시계열,time_series
줄기-잎_그림,stem-and-leaf_plot 페이지명으로는 간단히 stemplot 정도가 나을듯 ... WtEn:stemplot ... 줄기그림,stemplot ?
{
AKA 줄기-잎 도표
줄기와 잎 그림

중소규모의 데이터 집합 구성에 적합함.


[https]수학백과: 줄기와 잎 그림
}// 줄기와 잎 그림 ... Ggl:줄기와 잎 그림 Bing:줄기와 잎 그림
히스토그램,histogram
{
계급,class을 가로로 하고 그 계급의 도수(빈도수 frequency - 빈도,frequency)를 세로로 하는 직사각형으로 나타낸 그래프,graph.
히스토그램의 각 직사각형의 윗변의 중점을 차례대로 선분으로 연결하면 도수분포다각형이 된다.
주의: 상자의 면적이 상대도수임 (높이가 아님)







표준측도(Z-score)
{
from http://www.kocw.net/home/search/kemView.do?kemId=1162312 2장. 자료의 표현_변동성
$z=\frac{x-\bar{x}}{s}$
s: 표준편차,standard_deviation
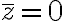그러면 z의 평균 $\bar{z}=0$ 이고 분산=1
}
변동계수,variation_coefficient

(기타 각종 알파벳으로 시작하는것들)
z-test
{
두 집단의 평균비교를 통한 가설을 검증하는 분석기법 // 가설검증이란 가설검정,hypothesis_test? chk
}
p-value p값
{
//from mathworld
{
"The probability that a variate would assume a value greater than or equal to the observed_value strictly by chance : P(z≥zobserved)
-> 변량,variate, 관찰,observation, observed_value, 값,value
rel. significance https://mathworld.wolfram.com/Significance.html
rel. alpha_value https://mathworld.wolfram.com/AlphaValue.html
}
rel. 귀무가설,null_hypothesis, ..
https://mathworld.wolfram.com/P-Value.html
[https]수학산책: P-value
WpEn:P-value
WpKo:유의_확률
Up: 값,value(이름), 확률,probability
}
R제곱 R_square R_squared? R2
{
회귀 직선의 방정식이 얼마나 원래의 자료를 잘 설명하는지 나타내는 수치
Google:r square
}
i.i.d., iid
{
// RR:i.i.d.
}






[edit]

2. 평균, 분산, 표준편차

이산확률변수 X의 기댓값 또는 평균(평균,mean,average):
$E(X)=x_1p_1+x_2p_2+\cdots+x_np_n=\sum x_i p_i $

이산확률변수 X의 분산,variance:
$V(X)=E((X-m)^2)=\sum (x_i-m)^2 p_i$
분산을 구하는 다른 방법(증명은 아래에):
$V(X)=E(X^2)-(E(X))^2=\sum x_i^2 p_i-m^2$

이산확률변수 X의 표준편차,standard_deviation:
$\sigma(x)=\sqrt{V(X)}$

[edit]

2.1. 증명

  • $V(X)=\sum(x_i-m)^2p_i$ 뿐만 아니라 $V(X)=\sum(x_i^2p_i)-m^2$ 인 이유
  • $V(X)=E((X-m)^2)$ 뿐만 아니라 $V(X)=E(X^2)-(E(X))^2$ 인 이유

먼저
$\sum p_i = 1$
$\sum x_i p_i = m$ 이다.

$V(X)= \sum(x_i-m)^2p_i$
$=\sum(x_i^2-2mx_i+m^2)p_i$
$=\sum x_i^2p_i - 2m\sum x_i p_i + m^2\sum p_i$
$=\sum x_i^2p_i - 2m^2 + m^2$
$=\sum x_i^2p_i - m^2$
$=E(X^2)-(E(X))^2$


[edit]

3. 상관 correlation

[edit]

4. tmp links ko

blog postings
https://blog.naver.com/gogocj2012/ - 알기쉬운 통계학



[edit]

5. See also