'(값−평균)2의 평균'. (나가노 히로유키)
// ㄷㄱㄱ Week 6-2 p9
Variance: a fixed value that represents how much a RV can vary
Continuous RV의 경우:
Variance: a fixed value that represents how much a RV can vary
Var[X]=σX2=E[(X−E[X])2]=E[X2]−E[X]2
![$\text{Var}[X]=\sigma_X^2=\text{E}[(X-\text{E}[X])^2]=\text{E}[X^2]-\text{E}[X]^2$ $\text{Var}[X]=\sigma_X^2=\text{E}[(X-\text{E}[X])^2]=\text{E}[X^2]-\text{E}[X]^2$](/123/cgi-bin/mimetex.cgi?\Large \text{Var}[X]=\sigma_X^2=\text{E}[(X-\text{E}[X])^2]=\text{E}[X^2]-\text{E}[X]^2)
Discrete RV의 경우:Continuous RV의 경우:
편차의 제곱의 평균이란? 단계적으로 보면
편차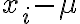
편차의 제곱^2)
편차의 제곱의 평균^2) ← 분산
← 분산
편차
편차의 제곱
편차의 제곱의 평균
....근데 표본분산이라면 분모에 n-1 들어감...chk
^2) CHK
CHK
1. 설명 ¶
분산을 구하는 순서
 개의 데이터
개의 데이터
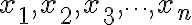
가 있을 때, 분산은
^2 + (x_2-\bar{x})^2 + (x_3-\bar{x})^2 + \cdots + (x_n-\bar{x})^2}{n})
i.e.
^2)
아울러 표준편차,standard_deviation는 물론
^2 + (x_2-\bar{x})^2 + (x_3-\bar{x})^2 + \cdots + (x_n-\bar{x})^2}{n}})
그렇다면 확률변수,random_variable의 분산은?
=E(X^2)-(E(X))^2)
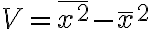
이것의 증명은,
=E((X-\bar{X})^2))
^2 p_i)
p_i)
) (여기서
(여기서 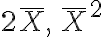 은 상수이므로
은 상수이므로 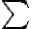 앞에 놓을 수 있다.)
앞에 놓을 수 있다.)
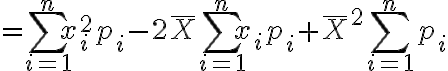 (여기서
(여기서  이므로)
이므로)
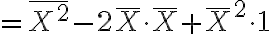
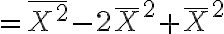
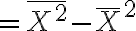
-(E(X))^2)
(나가노 히로유키)
- 데이터의 평균을 구한다
- 각 데이터에 대해, (값 − 평균)을 구한다
- 각 데이터의 (값 − 평균)2을 구한다
- (값 − 평균)2의 평균을 구한다
"제곱의 평균 빼기 평균의 제곱"으로 계산 가능
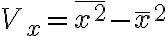
=E(X^2)-(E(X))^2)
두번째 적률(2nd moment)임. See 적률,moment
6. 표본분산 sample variance ¶
7. sampling variance ¶
9. 공분산 covariance ¶
공분산,covariance - 확률변수가 두 개 이상일 때? - yes
//tmp chk; from https://blog.naver.com/ivivaldi/221930184691 ... 공분산과 주성분분석. CLEANUP and TOMOVE, TOFORK.
{
분산과의 관계
{
분산과의 관계
분산 variance : 한 random variable
공분산 covariance : 두 개 이상의 random variable
공분산 covariance : 두 개 이상의 random variable
.....
공분산행렬covariance_matrix 은 semi-definite_matrix { 준정부호행렬 또는 준정치행렬 ? } 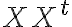 를 써서 이렇게 표현 가능
를 써서 이렇게 표현 가능
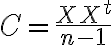
그리고 C의 크기는 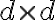 ... 표본 개수와 관계없이 확률변수의 개수(차원)로만 표현된다.
... 표본 개수와 관계없이 확률변수의 개수(차원)로만 표현된다.
covariance_matrix 의
...
대각선 성분은 variance,
그 이외 성분은 correlation(redundancy) 이다.
// 상관,correlation(curr see 상관계수,correlation_coefficient) 여유도,redundancy
데이터,data를 다룰 때 correlation(redundancy)를 최소화하고 variance를 최대화하여 데이터를 압축,compression한다.그 이외 성분은 correlation(redundancy) 이다.
// 상관,correlation(curr see 상관계수,correlation_coefficient) 여유도,redundancy
...
PCA와 특이값분해,singular_value_decomposition,SVD의 관계.
위
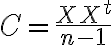
을 대각행렬,diagonal_matrix로 표현하면,
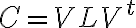
V 행렬의 각 열,column이 고유벡터,eigenvector다.
L 행렬의 대각선성분(주대각선 주대각성분 main_diagonal
주대각성분 main_diagonal  대각원소 diagonal_element s diagonal_entry -ies ? ) 은 대각선 방향으로 감소하는 고유값,eigenvalues들
대각원소 diagonal_element s diagonal_entry -ies ? ) 은 대각선 방향으로 감소하는 고유값,eigenvalues들  이다.
이다.
고유벡터는 data의 'principal_axis' or 'principal_direction's 이다.
data의 principle axes로의 사영,projection을 principal_component s (PC scores)라고 한다.
위
L 행렬의 대각선성분(주대각선
고유벡터는 data의 'principal_axis' or 'principal_direction's 이다.
data의 principle axes로의 사영,projection을 principal_component s (PC scores)라고 한다.
V 행렬의 각 열이 고유벡터라는 것은, 다시 말해 고유벡터열 eigenvector_column 의 확장공간(생성,span)으로 데이터를 표현할 수 있다는 것이고,
이 span으로 data를 투영(projection?)하여 data를 근사화(see 근사,approximation)할 수 있다.
이 span으로 data를 투영(projection?)하여 data를 근사화(see 근사,approximation)할 수 있다.
여기서 기저벡터(기저,basis)를 다 쓰지 않고 'data의 90% 특성을 반영하는'(QQQ 정확한 뜻 i.e. 수량적/정량적 정의?) 일부 기저벡터만 이용하면 저차원(low-dimension)데이터로 압축된다.
즉 차원을 줄여 정보량을 줄인다 => 압축한다 ? chk
즉 차원을 줄여 정보량을 줄인다 => 압축한다 ? chk
데이터 X를 SVD로 표현하고 위 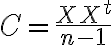 에 대입하면
에 대입하면
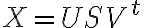
여기서
U는 유니터리행렬,unitary_matrix이고,
S는 대각행렬,diagonal_matrix of singular values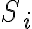 (? chk)
(? chk)
U는 유니터리행렬,unitary_matrix이고,
S는 대각행렬,diagonal_matrix of singular values
singular_value s 는 공분산행렬,covariance_matrix 의 고유값,eigenvalue과 다음 관계를 가진다.
}
11. 기타 ¶
PL에서 *variance (covariance, contravariance) 에 대해서는 여길 참조  Covariance_and_contravariance_(computer_science)
Covariance_and_contravariance_(computer_science)
https://mathworld.wolfram.com/Variance.html
![[https]](/123/imgs/https.png) 수학백과: 분산
수학백과: 분산
 Variance
Variance
 분산
분산
 Variance
Variance
https://everything2.com/title/Variance
![[https]](/123/imgs/https.png) 수학백과: 분산
수학백과: 분산https://everything2.com/title/Variance
같은 한국어 분산, 다른 영어: 분산,dispersion

