AKA integral calculus
이 때
Sub:
정적분,definite_integral
부정적분,indefinite_integral
치환적분,integration_by_substitution
부분적분,integration_by_parts
경로적분,contour_integral
이상적분,improper_integral
중적분,multiple_integral and 반복적분,repeated_integral and 반복적분,iterated_integral - 아래 중적분 section에 언급
수치적분,numerical_integration - 정적분으로 mv?
적분표,integral_table
적분변환,integral_transform
라이프니츠_적분규칙,Leibniz_integral_rule
적분인자,integrating_factor부정적분,indefinite_integral
치환적분,integration_by_substitution
부분적분,integration_by_parts
경로적분,contour_integral
이상적분,improper_integral
중적분,multiple_integral and 반복적분,repeated_integral and 반복적분,iterated_integral - 아래 중적분 section에 언급
수치적분,numerical_integration - 정적분으로 mv?
적분표,integral_table
적분변환,integral_transform
라이프니츠_적분규칙,Leibniz_integral_rule
LinkThese....
{
Antonym(반의어), 역연산: 미분,derivative or 미분,differential?
}
{
Antonym(반의어), 역연산: 미분,derivative or 미분,differential?
| 미분 | 도함수를 구하기 |
| 적분 | 역도함수(원시함수)를 구하기 |
Sub:
리만_적분,Riemann_integral 작성중
르베그_적분,Lebesgue_integral 작성중
Stieltjes_integral 작성중
다르부_적분,Darboux_integral - 리만적분과...
라플라스_적분,Laplace_integral - tbw, 현재 푸리에_변환,Fourier_transform에서만 언급
다니엘_적분,Daniell_integral - writing
이토_적분,Ito_integral - writing
Wiener_integral - writing
Stratonovich_integral - writing
Skorokhod_integral - Ito의 확장 - writing
strong_integral - writing
Pettis_integral - writing
Bochner_integral - writing
르베그_적분,Lebesgue_integral 작성중
Stieltjes_integral 작성중
다르부_적분,Darboux_integral - 리만적분과...
라플라스_적분,Laplace_integral - tbw, 현재 푸리에_변환,Fourier_transform에서만 언급
다니엘_적분,Daniell_integral - writing
이토_적분,Ito_integral - writing
Wiener_integral - writing
Stratonovich_integral - writing
Skorokhod_integral - Ito의 확장 - writing
strong_integral - writing
Pettis_integral - writing
Bochner_integral - writing
Contents
1. 적분 표기 및 기호 ¶
CHK
{
integral에 동그라미가 있으면,
![[https]](/123/imgs/https.png) src
src
{
integral에 동그라미가 있으면,
∮ : 닫힌 경로(닫힌경로,closed_path)? 곡선(폐곡선)? 에 대한 적분일 때. 선적분,line_integral over a closed 곡선,curve(닫힌곡선,closed_curve) (for line integrals over a closed curve.)
∯ : 닫힌 곡면 (폐곡면)에 대한 적분일 때. 면적분,surface_integral over a closed 곡면,surface(닫힌곡면,closed_surface)
via ∯ : 닫힌 곡면 (폐곡면)에 대한 적분일 때. 면적분,surface_integral over a closed 곡면,surface(닫힌곡면,closed_surface)
![[https]](/123/imgs/https.png) src
src3. 중적분 multiple integral ¶
독립변수가 2개 이상인 함수를 적분하는 것
푸비니_정리,Fubini_theorem - writing
반복적분,repeated_integral https://mathworld.wolfram.com/RepeatedIntegral.html
과 차이? - (2022-02-13) mw 보면,
이것도 kms에서 반복적분이라 하는데, 위와 차이 있음? 같은거?
과 차이? - (2022-02-13) mw 보면,
- repeated integral - multiple times over a single variable
- multiple integral - w.r.t different variables
이것도 kms에서 반복적분이라 하는데, 위와 차이 있음? 같은거?
Twins:
https://mathworld.wolfram.com/MultipleIntegral.html
https://encyclopediaofmath.org/wiki/Multiple_integral
 Multiple_integral
Multiple_integral
 중적분
중적분
 중적분
중적분
https://angeloyeo.github.io/2020/07/30/multiple_integral.html
https://mathworld.wolfram.com/MultipleIntegral.html
https://encyclopediaofmath.org/wiki/Multiple_integral
https://angeloyeo.github.io/2020/07/30/multiple_integral.html
Up: 적분,integration
3.4. 면적분 surface integral ¶
3.5. 부피적분 volume integral ¶
AKA 체적적분
//mw 내용 매우 짧으므로 그대로 써보면:
{
A 삼중적분,triple_integral over three coord.s giving the 부피,volume within some 영역,region
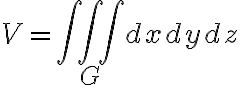
}
{
A 삼중적분,triple_integral over three coord.s giving the 부피,volume within some 영역,region
Misc
kms단어는 체적적분. 부피적분이라 하지 않은 이유는?
kms단어는 체적적분. 부피적분이라 하지 않은 이유는?
4. 경로적분 ¶
으로 번역되는 단어는 contour/path integral이 있음.
- contour integral - 유수 정리 (residue theorem)와 관련
Go to 경로적분,contour_integral
- path integral 경로적분
- Feynman path integral 파인만 경로적분
- Wiener path integral 위너 경로적분
- Feynman path integral 파인만 경로적분
5. 편적분 ¶
편미분,partial_derivative의 반대. 특정 문자에 대해서만 (다른 문자는 상수로 보고) 적분하는 것.
이것은 특이하게도 검색하면 별로 안 나온다. 왜지?
용어가 따로 있는 것인가, 아님 편미분을 알면 너무 trivial한 개념이라 별도 항목으로 설명하고 있는 곳이 없는 것인가?
partial integration을 검색하면 부분적분,integration_by_parts이 나옴.
이것은 특이하게도 검색하면 별로 안 나온다. 왜지?
용어가 따로 있는 것인가, 아님 편미분을 알면 너무 trivial한 개념이라 별도 항목으로 설명하고 있는 곳이 없는 것인가?
partial integration을 검색하면 부분적분,integration_by_parts이 나옴.
(Stewart 8e ko p823)
6. 적분의 성질 properties of integration ¶
단조수렴정리(MCT) monotone convergence theorem
지배수렴정리(DCT) dominated convergence theorem
유계수렴정리(BCT) bounded convergence theorem
https://seoncheolpark.github.io/book/_book/6-4-properties-of-integration.html
지배수렴정리(DCT) dominated convergence theorem
유계수렴정리(BCT) bounded convergence theorem
https://seoncheolpark.github.io/book/_book/6-4-properties-of-integration.html
7. 적분가능, 적분가능성, 적분불가능, .. ¶
Compare: 미분가능(성). see 미분,differentiation#s-3
표현
integrability 적분가능성 - mk page 적분가능성,integrability? - ok. 작성중
integrable 적분가능한
integrability theorem 적분가능 정리
Riemann integrable 리만 적분가능한
// from![[http]](/123/imgs/http.png) kms '적분가능' 검색
kms '적분가능' 검색
integrability 적분가능성 - mk page 적분가능성,integrability? - ok. 작성중
integrable 적분가능한
integrability theorem 적분가능 정리
Riemann integrable 리만 적분가능한
// from
![[http]](/123/imgs/http.png) kms '적분가능' 검색
kms '적분가능' 검색정의가 이상적분,improper_integral 값이 무한한지 여부로... TBW
TBD: 절대적분,absolute_integration page needed?
QQQ:
절대적분가능성은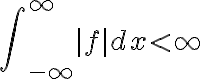 라는데 그럼
라는데 그럼
적분가능성은 ?
?
절대적분가능성은
적분가능성은
Sub:
절대적분가능함수 absolutely_integrable_function
{
absolutely integrable function
절대적분가능함수 absolutely_integrable_function
{
absolutely integrable function
구간,interval을 분할,partition하고, 각 부분구간,subinterval에서 임의로 한 점,point을 택해 표본점,sample_point이라 하고, 리만_합,Riemann_sum을 정의. 리만합의 극한이 존재하면 적분가능하며 그 적분값을 정적분으로 정의.
7.1. 정리: 연속함수의 적분가능성 ¶
만일 함수  가 구간
가 구간 ![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) 에서 연속, 또는
에서 연속, 또는  가 그 구간에서 기껏해야 유한개의 도약불연속점만을 갖는다면, 정적분
가 그 구간에서 기껏해야 유한개의 도약불연속점만을 갖는다면, 정적분 dx) 는 존재하고
는 존재하고  는 구간
는 구간 ![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) 에서 적분가능하다.
에서 적분가능하다.
Dirichlet_function는 리만 적분을 갖지 못한다. 상합과 하합이 서로 다른 극한값으로 수렴.
(Thomas 13e ko p254)
Dirichlet_function는 리만 적분을 갖지 못한다. 상합과 하합이 서로 다른 극한값으로 수렴.
(Thomas 13e ko p254)
9. 푸리에 적분 Fourier integral ¶
curr at 푸리에_해석,Fourier_analysis
Q: 다음 단어의 의미차는?
integration
integral
페이지명 integral에서 integration으로 바꿈.
integration
integral
페이지명 integral에서 integration으로 바꿈.
아주 대충,
integration is_a: 연산,operation(반대 개념은 반대 연산(or 역연산 ... inverse_operation / rel inverse_operator)인 미분,differentiation),
integral is_a: 결과,result(반대 개념은 도함수=미분,derivative) (정적분일 경우 값 / 부정적분일 경우 함수(esp 도함수 derivative))
인 듯 한데 rechk later ...
+ 범함수,functional, 변환,transformation esp 적분변환,integral_transform과의 비교/차이점 tbw...? 필요 있나? (아주 대충만 서술하면 범함수는 함수의 일종, 근데 뜻이 다양하서 짧게 서술 불가능하네... 아무튼 입력,input(≃argument≃parameter)이 함수라는 공통점. (예외 있는지 chk) 변환도 생각하보니 뜻이 분야에 따라 너무 다양.)
integral is_a: 결과,result(반대 개념은 도함수=미분,derivative) (정적분일 경우 값 / 부정적분일 경우 함수(esp 도함수 derivative))
인 듯 한데 rechk later ...
+ 범함수,functional, 변환,transformation esp 적분변환,integral_transform과의 비교/차이점 tbw...? 필요 있나? (아주 대충만 서술하면 범함수는 함수의 일종, 근데 뜻이 다양하서 짧게 서술 불가능하네... 아무튼 입력,input(≃argument≃parameter)이 함수라는 공통점. (예외 있는지 chk) 변환도 생각하보니 뜻이 분야에 따라 너무 다양.)
적분관련 단어들/표현들 추가예정
 Integration
Integration
 Integral
Integral
https://ncatlab.org/nlab/show/integral
- integrand 적분될 함수, 피적분함수[1]
 integrand#Noun https://ncatlab.org/nlab/show/integrand
integrand#Noun https://ncatlab.org/nlab/show/integrand
https://ncatlab.org/nlab/show/integral
Up: 미적분,calculus

