curved* (such as curved line / curved surface / etc.)
chk, 내생각, tmp
{
QQQ: 곡선은 1차원, 곡면은 2차원, 계속 확장 가능? 곡부피(?)는 3차원, (?)은 (??)차원, ... (???)
{
QQQ: 곡선은 1차원, 곡면은 2차원, 계속 확장 가능? 곡부피(?)는 3차원, (?)은 (??)차원, ... (???)
평면곡선은 parameter 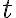 에 대해
에 대해 ,y(t))) 로 볼 수 있는데 이게 정의? (이희원) Or, 매개곡선,parametric_curve(rel. 매개변수방정식,parametric_equation) only? 아님 이게 일반적이므로 이게 정의로 적당한..?
로 볼 수 있는데 이게 정의? (이희원) Or, 매개곡선,parametric_curve(rel. 매개변수방정식,parametric_equation) only? 아님 이게 일반적이므로 이게 정의로 적당한..?
}
}
연필을 떼지 않고 한번에 그릴 때 시작-끝 점이 같음, i.e. 시점과 종점이 일치
곡선의 시점과 종점이 같을 경우, 즉 =\vec{r}(a)) 인 곡선을 닫힌곡선(closed curve)이라 한다. (Stewart)
인 곡선을 닫힌곡선(closed curve)이라 한다. (Stewart)
단일곡선,simple_curve ... 2022-07-12 : 단순곡선,simple_curve으로 작성중 ... 단일은 double 그 이상이 아닌 'single'에 더 어울리는 듯, '스스로 교차하지 않음'이라는 뜻에 잘 어울리지는 않는 듯?
{
simple curve
같은 점을 두 번 이상 지나지 않음 i.e. 교차하지 않음
(Kreyszig 번역판:) 중복점(multiple point)이 없는 곡선, 즉 자신과 교차하거나 접하는 점이 없는 곡선을 단순곡선(simple curve)이라 한다. 원이나 나선은 단순곡선이다.
https://mathworld.wolfram.com/SimpleCurve.html
}
{
simple curve
같은 점을 두 번 이상 지나지 않음 i.e. 교차하지 않음
(Kreyszig 번역판:) 중복점(multiple point)이 없는 곡선, 즉 자신과 교차하거나 접하는 점이 없는 곡선을 단순곡선(simple curve)이라 한다. 원이나 나선은 단순곡선이다.
https://mathworld.wolfram.com/SimpleCurve.html
}
단일폐곡선,simple_closed_curve ... 단순닫힌곡선 ?
{
simple closed curve
폐곡선 ∩ 단일곡선
closed_curve ∩ simple_curve
원과 위상동형(homeomorphic) - see 위상동형사상,homeomorphism
Examples: 원,circle, 타원,ellipse,
{
simple closed curve
폐곡선 ∩ 단일곡선
closed_curve ∩ simple_curve
원과 위상동형(homeomorphic) - see 위상동형사상,homeomorphism
Examples: 원,circle, 타원,ellipse,
}
//위아래 같은건지? chk - yes. via
![[https]](/123/imgs/https.png) 두산백과 단일폐곡선
두산백과 단일폐곡선조르당_곡선,Jordan_curve
{
Jordan curve
평면,plane에 있는 곡선으로 안과 밖을 둘,2로 구분/이분한다(분할,partition > 이분,bipartition).
관련 정리: 조르당_곡선정리,Jordan_curve_theorem - 안쪽,inside과 바깥쪽,outside이 경계,boundary
}
https://mathworld.wolfram.com/JordanCurveTheorem.html
 Jordan_curve_theorem
Jordan_curve_theorem
 조르당_곡선_정리
조르당_곡선_정리
Up: algebraic_topology
https://mathworld.wolfram.com/JordanCurve.htmlUp: algebraic_topology
}
매끄러운곡선,smooth_curve
{
매끄러운 곡선, smooth curve
경로적분,contour_integral에서 언급되는데 TBW. 선적분,line_integral과도 관련있는듯
mklink 매끄러운함수,smooth_function
https://mathworld.wolfram.com/SmoothCurve.html
Up: 매끄러움,smoothness
}
{
매끄러운 곡선, smooth curve
경로적분,contour_integral에서 언급되는데 TBW. 선적분,line_integral과도 관련있는듯
mklink 매끄러운함수,smooth_function
https://mathworld.wolfram.com/SmoothCurve.html
Up: 매끄러움,smoothness
}
원뿔곡선,conic_section (=이차곡선,quadratic_curve? 아님 그 일종?)
호,arc
사이클로이드,cycloid
에피사이클로이드,epicycloid
하이포사이클로이드,hypocycloid
현수선,catenary
심장형 cardioid (writing)
astroid (writing)
{
![[https]](/123/imgs/https.png) 수학백과: 렘니스케이트
수학백과: 렘니스케이트
이것은 Cassini_oval(![[https]](/123/imgs/https.png) 수학백과: 카시니 난형선 or 카시니 타원 { 두 정점까지의 거리의 곱이 일정한 점들의 집합 } 의 특수한 경우.
수학백과: 카시니 난형선 or 카시니 타원 { 두 정점까지의 거리의 곱이 일정한 점들의 집합 } 의 특수한 경우.
 Lemniscate
Lemniscate
 렘니스케이트
렘니스케이트
}
devil's curve
kampyle of Eudoxus
Tschirnhausen cubic
타원곡선,elliptic_curve
나선,helix
{
Ex. 원나선(circular helix)
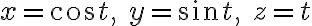
영어 발음 헬릭스가 아닌 힐릭스.
}
,spiral - 이것도 나선으로 번역되는 일이 자주 (eg kms![[https]](/123/imgs/https.png) https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=spiral)
https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=spiral)
{
The Hypnotic World of Degenerate Spirals
https://www.dogatekin.com/blog/hypnotic-degenerate-spirals/
https://news.ycombinator.com/item?id=27097719
호,arc
사이클로이드,cycloid
에피사이클로이드,epicycloid
하이포사이클로이드,hypocycloid
현수선,catenary
심장형 cardioid (writing)
astroid (writing)
astroid = hypocycloid of four cusps - ex. 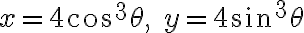 (Stewart 9e 10.2 바로 앞)
(Stewart 9e 10.2 바로 앞)
렘니스케이트,lemniscate{
![[https]](/123/imgs/https.png) 수학백과: 렘니스케이트
수학백과: 렘니스케이트이것은 Cassini_oval(
![[https]](/123/imgs/https.png) 수학백과: 카시니 난형선 or 카시니 타원 { 두 정점까지의 거리의 곱이 일정한 점들의 집합 } 의 특수한 경우.
수학백과: 카시니 난형선 or 카시니 타원 { 두 정점까지의 거리의 곱이 일정한 점들의 집합 } 의 특수한 경우.}
devil's curve
kampyle of Eudoxus
Tschirnhausen cubic
타원곡선,elliptic_curve
나선,helix
{
Ex. 원나선(circular helix)
}
,spiral - 이것도 나선으로 번역되는 일이 자주 (eg kms
![[https]](/123/imgs/https.png) https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=spiral)
https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=spiral){
The Hypnotic World of Degenerate Spirals
https://www.dogatekin.com/blog/hypnotic-degenerate-spirals/
https://news.ycombinator.com/item?id=27097719
AKA 스파이럴
}
// wpko에선 각각 spiral은 와선, helix는 나선으로 번역.
// spiral Spiral
Spiral  와선 (소용돌이선, 달팽이선) - nautilus, ...
와선 (소용돌이선, 달팽이선) - nautilus, ...
// helix Helix
Helix  나선 - double helix는 DNA에서, ...
나선 - double helix는 DNA에서, ...
데카르트의 엽선 folium of Descartes
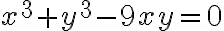
etc.
}
// wpko에선 각각 spiral은 와선, helix는 나선으로 번역.
// spiral
// helix
데카르트의 엽선 folium of Descartes
분류를 해야 하는데.
매개곡선,parametric_curve (매개변수곡선) - 관련: 매개변수방정식,parametric_equation
평면상에 있지 않은 곡선: 뒤틀린 곡선(twisted curve)
매개곡선,parametric_curve (매개변수곡선) - 관련: 매개변수방정식,parametric_equation
conchoids of Nicomedes
극곡선,polar_curve - 관련: 극방정식,polar_equationlimaçon 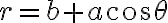
ovals of Cassini
평면,plane상의 곡선: 평면곡선(plane curve)ovals of Cassini
평면상에 있지 않은 곡선: 뒤틀린 곡선(twisted curve)
1. 관련 또는 주제 ¶
곡선 관련 개념, 혹은 곡선에 대한 주제들(topics)
kms torsion : https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=torsion
{2023-12-18 "torsion : 비틀림(률), 꼬임(률)"}
{2023-12-18 "torsion : 비틀림(률), 꼬임(률)"}
경로,path: 실수 구간,interval을
궤적,trajectory
{
위상평면,phase_plane을 식(매개변수방정식,parametric_equation)의 궤적들로 채우면, 식의 위상투영(phase portrait)을 얻는다.
궤적과 비슷한 표현은 궤도,orbit, 경로,path.
(Kreyszig 10e 4.3 위상평면법)
궤적,trajectory
{
위상평면,phase_plane을 식(매개변수방정식,parametric_equation)의 궤적들로 채우면, 식의 위상투영(phase portrait)을 얻는다.
궤적과 비슷한 표현은 궤도,orbit, 경로,path.
(Kreyszig 10e 4.3 위상평면법)
Frenet_frame,프레네_틀 - Frenet-Serret,TNB에 작성중
{
TNB frame이랑 동의어인가? chk
TNB_vector
 프레네-세레_공식
프레네-세레_공식
 Frenet–Serret_formulas
Frenet–Serret_formulas
{
TNB frame이랑 동의어인가? chk
TNB_vector
이런 것들이 다 같은 말을 하고 있는듯 chk
대충, 3D에서 곡률(곡률,curvature, 얼마나 curvy)뿐만 아니라 (얼마나 구불구불한지 twisty)를 측정하는 그런 개념?
from https://youtu.be/gsUgDpGWk-M 5분쯤
from https://youtu.be/gsUgDpGWk-M 5분쯤
여기서 torsion 개념이 나온다.
{
torsion을 kms에서 검색하면 "비틀림(률), 꼬임(률)"
Definition: torsion τ
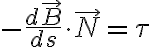
τ = 0 : no twisting
{
torsion을 kms에서 검색하면 "비틀림(률), 꼬임(률)"
Definition: torsion τ
κ(curvature) shows how points "curve" in the plane defined by 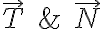
τ(torsion) shows how that plane "twists"
τ(torsion) shows how that plane "twists"
공간곡선을 다룰 때 세 벡터 T, N, B를 사용한 해석법
AKA 프레네-세레 틀, Frenet-Serret frame, TNB_frame
단위접벡터,unit_tangent_vector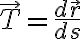
단위법선벡터,unit_normal_vector
단위이중법선벡터 unit_binormal_vector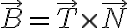
from https://suhak.tistory.com/922
AKA 프레네-세레 틀, Frenet-Serret frame, TNB_frame
단위접벡터,unit_tangent_vector
단위법선벡터,unit_normal_vector
단위이중법선벡터 unit_binormal_vector
from https://suhak.tistory.com/922
벡터,vector페이지에서 "binormal vector" 검색하면 관련 짧은 내용 있음. 저기선 종법선벡터로 번역.
kms 찾아보니 저 단어는 "이중수직벡터", "종법선벡터" 두 결과가 나옴. 즉 통일 안됨.
kms 찾아보니 저 단어는 "이중수직벡터", "종법선벡터" 두 결과가 나옴. 즉 통일 안됨.
2. 비교 ¶
직선,line
직선도 곡률이 ()인 곡선인가? 아님 반대 개념인가?
곡선의 차원,dimension을 확장하면, 곡면,surface직선은 곡선의 일종으로, 곡률이 0인 곡선으로 보는 게 타당한 듯.
3. 곡선의 접선(tangent) ¶
곡선 C 위에 정점 P와 이 곡선을 따라 P로 접근하는 점 Q가 있다면, 점 P에서의 접선은, P와 Q를 지나는 직선,line L ) 의 극한으로 정의.
의 극한으로 정의.
곡선 C가) 로 표현되고 점
로 표현되고 점 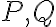 가 각각
가 각각 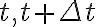 에 대응된다면 다음 벡터는
에 대응된다면 다음 벡터는 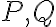 를 잇는 직선 L과 같은 방향이다.
를 잇는 직선 L과 같은 방향이다.
![$\frac{1}{\Delta t}[\vec{r}(t+\Delta t)-\vec{r}(t)]$ $\frac{1}{\Delta t}[\vec{r}(t+\Delta t)-\vec{r}(t)]$](/123/cgi-bin/mimetex.cgi?\Large \frac{1}{\Delta t}[\vec{r}(t+\Delta t)-\vec{r}(t)])
) 가 미분가능하다고 가정. 그 극한은 도함수
가 미분가능하다고 가정. 그 극한은 도함수
=\lim_{\Delta t\to 0}\frac{\vec{r}(t+\Delta t)-\vec{r}(t)}{\Delta t})
가 된다. 만약 \ne 0) 이면
이면 ) 를 P에서 C의 접선벡터(see 접벡터,tangent_vector)라고 한다. 여기에 대응하는 단위벡터,unit_vector
를 P에서 C의 접선벡터(see 접벡터,tangent_vector)라고 한다. 여기에 대응하는 단위벡터,unit_vector
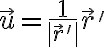
를 단위접벡터,unit_tangent_vector라 한다.
(Kreyszig 10e 9.5)
곡선 C가
(Kreyszig 10e 9.5)
4. 곡선의_길이 curve length ... = arclength arc_length ¶
구간 ![$[a,b]$ $[a,b]$](/123/cgi-bin/mimetex.cgi?\Large [a,b]) 에서
에서 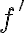 이 연속이면,
이 연속이면, 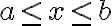 에서 곡선
에서 곡선 ) 의 길이는
의 길이는
)^2}dx)
곡선 C가  에 대해
에 대해 ,\,y=g(t)) 로 매개화되었고
로 매개화되었고 ) 와
와 ) 는 연속인 미분계수를 갖는다고 하면 곡선 C의 길이는
는 연속인 미분계수를 갖는다고 하면 곡선 C의 길이는
)^2+(g%27(t))^2}dt)
곡선의 길이 (Ivan)
곡선의 각 조각은 피타고라스정리에 의해
곡선 =(x(t),\ y(t),\ z(t))) 에서 구간
에서 구간  에 대응하는 곡선의 길이를 구해 보자.
에 대응하는 곡선의 길이를 구해 보자.
구간![$[a,\ b]$ $[a,\ b]$](/123/cgi-bin/mimetex.cgi?\Large [a,\ b]) 의 분할
의 분할 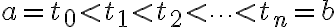 에 대응하는 곡선 위의 점을
에 대응하는 곡선 위의 점을 =(x(t_i),\ y(t_i),\ z(t_i))) 라고 하자.
라고 하자.
현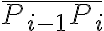 의 길이를
의 길이를 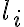 라고 하자.
라고 하자.
구간
현
곡선 C의 길이 L은 다음과 같다.
9. curve fitting, regression에서 말하는 curves ¶
curve_fitting (즉 rel. 보간,interpolation, 보외,extrapolation, 예측,prediction, 회귀,regression)
에서 다루는 곡선들을 회귀곡선,regression_curve이라 하고
이런 곡선을 찾는 과정을 회귀분석,regression_analysis이라 한다.
보통 least_squares가 많이 쓰이는 방법.
에서 다루는 곡선들을 회귀곡선,regression_curve이라 하고
이런 곡선을 찾는 과정을 회귀분석,regression_analysis이라 한다.
보통 least_squares가 많이 쓰이는 방법.
회귀곡선들에는 이런 게 있다.
직선,line
polynomial_curve - rel. 다항식,polynomial
 ... b가 자연수이면 polynomial_curve에 속하는건지?
... b가 자연수이면 polynomial_curve에 속하는건지?
exponential_curve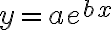
etc
polynomial_curve - rel. 다항식,polynomial
quadratic_curve 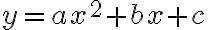
power_curve exponential_curve
etc
(Thomas 11e p64)
방법은 observed data(scatterplot으로 나타냄)에서 그것을 식,expression이 간단하면서도 가능한 한 잘 들어맞는 매끈한 곡선의 방정식(regression_equation)을 얻어내는? 그래서 그것을 (현상을 설명해주는) model로 삼는? - CHK
12. Links en ¶
3DXM Plane Curve Gallery
http://virtualmathmuseum.org/Curves/index.html
여러 곡선 갤러리 (interactive, javascript, animated)
http://virtualmathmuseum.org/Curves/index.html
여러 곡선 갤러리 (interactive, javascript, animated)
mathematical curves (2013)
a collection of 939 two-dimensional mathematical curves
https://www.2dcurves.com/
a collection of 939 two-dimensional mathematical curves
https://www.2dcurves.com/
14. 수학/물리학 밖의 곡선 ¶
기계학습,machine_learning쪽에서 이진분류기 binary_classifier 이진분류,binary_classification 성능 측정 관련인
ROC곡선,ROC_curve
ROC곡선,ROC_curve
비슷한? :
contour
KWs: arc length, 호의 길이, 현의 길이, line element(선소)
contour
KWs: arc length, 호의 길이, 현의 길이, line element(선소)
Up: 기하학,geometry

