방정식,equation (rev. 1.73)
See 공식,formula
see also 해석기하_공식
TODO 아래 분류가 제대로 안 되어있고 나열만 되어있는데, (ex. 미방인지 아닌지, 미방이라면 어떤 미방인지 etc.) 분류. - 가능할지? or 가치가 있을지? ex. 연립은 연립 밑에 모두 모을 가치가 있나?
see also 해석기하_공식
TODO 아래 분류가 제대로 안 되어있고 나열만 되어있는데, (ex. 미방인지 아닌지, 미방이라면 어떤 미방인지 etc.) 분류. - 가능할지? or 가치가 있을지? ex. 연립은 연립 밑에 모두 모을 가치가 있나?
어느 정도는 할 가치가 있을 듯
다만 트리형식으로 완벽 분류는 불가능, 여러 분류에 동시에 속하는 것이 많으므로
Contents
- 1. 대수방정식 algebraic equation
- 2. 연립방정식,system_of_equations
- 3. 극방정식 polar equation
- 4. 미분방정식,differential_equation
- 5. 맥스웰_방정식,Maxwell_s_equations
- 6. 파동방정식,wave_equation
- 7. 매개변수방정식,parametric_equation
- 8. 연속방정식,continuity_equation
- 9. 벡터방정식,vector_equation
- 10. 부정방정식,indeterminate_equation
- 11. Poisson and Laplace equation
- 12. 푸아송 방정식 Poisson equation
- 13. 라플라스 방정식 Laplace equation
- 14. 코시-리만 방정식 Cauchy–Riemann equation
- 15. 삼각방정식 trigonometric equation
- 16. 적분방정식 integral equation
- 17. Misc
- 18. Sites
1.1.1. 일차방정식(=선형방정식) ¶
선형대수에서는 상수항이 없는, 원점을 지나지 않는 경우를 매우 중시하는 듯..
이하 선형대수 관련.
{
이하 선형대수 관련.
{
형태는
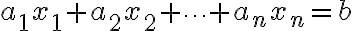
여기서
: 미지수.
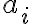: 계수. 모두 0이 되면 안된다.
특히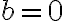 
인 경우를 특별히 homogeneous(동차, 제차) 선형방정식으로 부름.
다시 말해
일차방정식(linear equation):
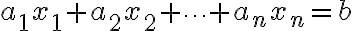(계수 모두 0인 경우 제외)
동차일차방정식(homogeneous linear equation):
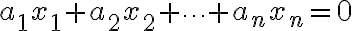(계수 모두 0인 경우 제외)
ex.
2차원 직선,line
 "$ax+by=c\;\;(a,b\ne0)$")
3차원 평면,plane
 "$ax+by+cz=d\;\;(a,b,c\ne0)$")
여러 개가 모여서(?) 연립방정식을 이루면, 선형방정식계(연립일차방정식,system_of_linear_equations).
Up:
}
일차방정식(linear equation):
2차원 직선,line
Up:
}
1계 선형미분방정식 first-order linear DE:
\frac{dy}{dx}+a_0(x)y=g(x) "$a_1(x)\frac{dy}{dx}+a_0(x)y=g(x)$")
여기서
=0 "$g(x)=0$")
: homogeneous 제차
otherwise : nonhomogeneous 비제차
그리고 이것의 standard form은,
y=f(x) "$\frac{dy}{dx}+P(x)y=f(x)$")
이것의 해,solution는 두 해의 합이라는 성질을 가지고 있다.
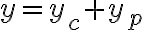
여기서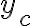 
는 다음 제차방정식의 해이다.
y=0 "$\frac{dy}{dx}+P(x)y=0$")
Homogeneous DE의 경우.
위 방정식은 분리가능하다.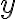
로 나누고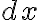 
를 곱하면
dx=0 "$\frac{dy}{y}+P(x)dx=0$")
풀면
dx} "$y_c=ce^{\textstyle-\int P(x)dx}$")
잠시 편의를 위해
 "$y_c=cy_1(x)$")
dx} "$y_1=e^{\textstyle-\int P(x)dx}$")
로 놓는다. 그리하여
y_1=0 "$\frac{dy_1}{dx}+P(x)y_1=0$")
이다. 이것을 사용하여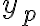 
를 찾을 것이다.
otherwise : nonhomogeneous 비제차
위 방정식은 분리가능하다.
Nonhomogeneous DE
variation_of_parameters { kms: 매개변수의 변분 / see https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=variation of / https://mathworld.wolfram.com/VariationofParameters.html } 방법을 써서 위의 standard form 방정식을 풀 것이다. 아이디어는 방정식의 해가 되는 즉 다음과 같은 함수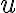
를 찾는 것이다.
y_1(x)=u(x)e^{\textstyle-\int P(x)dx} "$y_p=u(x)y_1(x)=u(x)e^{\textstyle-\int P(x)dx}$")
원래 방정식
← 
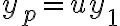대입
}{dx}+P(x)uy_1=f(x) "$\frac{d(uy_1)}{dx}+P(x)uy_1=f(x)$")
← 곱의 미분법칙 적용
uy_1=f(x) "$u\frac{dy_1}{dx}+y_1\frac{du}{dx}+P(x)uy_1=f(x)$")
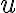← 로 묶는다
![$u\left[ \frac{dy_1}{dx}+P(x)y_1 \right]+y_1\frac{du}{dx}=f(x)$](/123/cgi-bin/mimetex.cgi?\Large u\left[ \frac{dy_1}{dx}+P(x)y_1 \right]+y_1\frac{du}{dx}=f(x) "$u\left[ \frac{dy_1}{dx}+P(x)y_1 \right]+y_1\frac{du}{dx}=f(x)$")
← 여기서 ![$[]$](/123/cgi-bin/mimetex.cgi?\Large [] "$[]$")
안이 0
 "$y_1\frac{du}{dx}=f(x)$")
변수분리하고 적분하면
}{y_1(x)}dx "$du=\frac{f(x)}{y_1(x)}dx$")
}{y_1(x)}dx "$u=\int\frac{f(x)}{y_1(x)}dx$")
 "$y_1(x)$")
의 정의에서부터, =e^{\textstyle\int P(x)dx} "$1/y_1(x)=e^{\textstyle\int P(x)dx}$")
이므로,
}{y_1(x)}dx\right)e^{\textstyle-\int P(x)dx}=e^{\textstyle-\int P(x)dx}\int e^{\textstyle\int P(x)dx} f(x)dx "$y_p=uy_1=\left(\int\frac{f(x)}{y_1(x)}dx\right)e^{\textstyle-\int P(x)dx}=e^{\textstyle-\int P(x)dx}\int e^{\textstyle\int P(x)dx} f(x)dx$")
dx}+e^{\textstyle-\int P(x)dx}\int e^{\textstyle\int P(x)dx} f(x)dx "$y=y_c+y_p=ce^{\textstyle-\int P(x)dx}+e^{\textstyle-\int P(x)dx}\int e^{\textstyle\int P(x)dx} f(x)dx$")
이것을 암기하려 하면 안된다. 식에 dx} "$e^{\textstyle\int P(x)dx}$")
를 곱하면
dx}y=c+\int e^{\textstyle\int P(x)dx} f(x)dx "$e^{\textstyle\int P(x)dx}y=c+\int e^{\textstyle\int P(x)dx} f(x)dx$")
미분하면
![$\frac{d}{dx}\left[e^{\textstyle\int P(x)dx}y\right]=e^{\textstyle\int P(x)dx}f(x)$](/123/cgi-bin/mimetex.cgi?\Large \frac{d}{dx}\left[e^{\textstyle\int P(x)dx}y\right]=e^{\textstyle\int P(x)dx}f(x) "$\frac{d}{dx}\left[e^{\textstyle\int P(x)dx}y\right]=e^{\textstyle\int P(x)dx}f(x)$")
dx}\frac{dy}{dx}+P(x)e^{\textstyle\int P(x)dx}y=e^{\textstyle\int P(x)dx}f(x) "$e^{\textstyle\int P(x)dx}\frac{dy}{dx}+P(x)e^{\textstyle\int P(x)dx}y=e^{\textstyle\int P(x)dx}f(x)$")
이것을 로 나누면 원래 방정식이 된다.
variation_of_parameters { kms: 매개변수의 변분 / see https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=variation of / https://mathworld.wolfram.com/VariationofParameters.html } 방법을 써서 위의 standard form 방정식을 풀 것이다. 아이디어는 방정식의 해가 되는 즉 다음과 같은 함수
1.1.3. 삼차방정식 cubic equation ¶
TBW:
삼차방정식 근과 계수와의 관계
삼차방정식 근과 계수와의 관계
판별식,discriminant은 이차방정식에 비해 지나치게 복잡하여 굳이 알아야 할지 의문.
See https://m.blog.naver.com/birth1104/222385891858
See https://m.blog.naver.com/birth1104/222385891858
1.1.5. 오차방정식 quintic equation ¶
4차방정식까지는 근의 공식이 있으나 5차 이상부터는 없다는 특징.
Why you can't solve quintic equations (Galois theory approach) #SoME2 - YouTube (Mathemaniac)
https://www.youtube.com/watch?v=zCU9tZ2VkWc
rel. 갈루아_이론,Galois_theory
https://www.youtube.com/watch?v=zCU9tZ2VkWc
rel. 갈루아_이론,Galois_theory
10. 부정방정식,indeterminate_equation ¶
해가 너무 많아서 정할 수 없는 방정식
미지수의 개수 > 식의 개수
디오판토스_방정식,Diophantine_equation - writing
디오판토스 방정식, Diophantine equation, 정수조건 부정방정식
2022-03-01
(주의)
부정방정식을 보면 이 단어는 정의가 제대로 확립되지 않은, ie 명확하지 않은 단어이다.
디오판토스 방정식, Diophantine equation, 정수조건 부정방정식
2022-03-01
(주의)
부정방정식을 보면 이 단어는 정의가 제대로 확립되지 않은, ie 명확하지 않은 단어이다.그리고 이하 links도 참고하여 제대로 page mk
Indeterminate_systemUnderdetermined_system interwiki: 
과소결정_연립방정식Overdetermined_system interwiki: 과결정_연립방정식
11. Poisson and Laplace equation ¶
이 둘이 밀접하여 같이 다루는 곳이 많아서 아직 분리 안함....
푸아송_방정식,Poisson_equation 2계편미방(wpko에는 2차편미방으로 되어 있는데 second order라는 것을 확인하고 수정. 역시 wpko는 믿을것이 못됨), elliptic pde; electrostatics 등에서 쓰임
Poisson's equation
https://mathworld.wolfram.com/PoissonsEquation.html
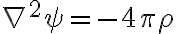
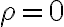이면 reduces to 라플라스방정식.
Up: 편미분방정식,partial_differential_equation,PDE
Poisson's equation
https://mathworld.wolfram.com/PoissonsEquation.html
라플라스_방정식,Laplace_equation
Laplace's equation
https://mathworld.wolfram.com/LaplacesEquation.html
Laplace's_equation
Up: 편미분방정식,partial_differential_equation,PDE
Laplace's equation
https://mathworld.wolfram.com/LaplacesEquation.html
Laplace's_equationUp: 편미분방정식,partial_differential_equation,PDE
tmp chk from https://m.blog.naver.com/seolgoons/221591886546 (가우스법칙, Poisson, Laplace)
{
가우스 법칙
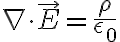
에,
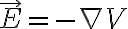
를 적용하면
=\frac{\rho}{\epsilon_0} "$\nabla\cdot(-\nabla V)=\frac{\rho}{\epsilon_0}$")
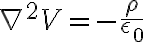
이렇게 Poisson eq가 나온다고.
{
가우스 법칙
}
https://m.blog.naver.com/seolgoons/221593432836 (Laplace)
https://freshrimpsushi.tistory.com/997 (Laplace and Poisson)
http://www.ktword.co.kr/abbr_view.php?m_temp1=4482&id=694
라플라스 방정식
https://m.blog.naver.com/seolgoons/221593432836 (Laplace)
https://freshrimpsushi.tistory.com/997 (Laplace and Poisson)
http://www.ktword.co.kr/abbr_view.php?m_temp1=4482&id=694
라플라스 방정식Poisson’s equation 푸아송_방정식
![[https]](/123/imgs/https.png)
여기(박석재)서 몇번 언급됨 (역학/중력 쪽 얘기. 물질분포와 가우스정리에서부터 처음 언급.)
그 바로 다음 파트에서는 전자기와 관련 언급됨.
푸아송_방정식라플라스 일반화라는 말의 뜻? 라플라스보다 더 일반적인 방정식??
Poisson eq.는 여기(박석재)서 몇번 언급됨 (역학/중력 쪽 얘기. 물질분포와 가우스정리에서부터 처음 언급.)그 바로 다음 파트에서는 전자기와 관련 언급됨.라플라스 방정식의 해는 조화함수,harmonic_function.
tmp links ko
{
전자기학 10) 전위,electric_potential와 라플라스_방정식
https://m.blog.naver.com/cindyvelyn/222044671663
1, 2, 3차원 라플라스 방정식 모양은 각각:
 "$\nabla^2V=\frac{\partial^2V}{\partial x^2}=0\;\;\;(=\frac{d^2V}{dx^2})$")
(변수가 하나이므로 ∂=d)
{
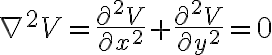
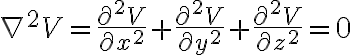
전자기학 10) 전위,electric_potential와 라플라스_방정식
https://m.blog.naver.com/cindyvelyn/2220446716631, 2, 3차원 라플라스 방정식 모양은 각각:
전자기학 11) 전자기학의 유일성 정리 https://m.blog.naver.com/cindyvelyn/222051213345
유일성정리(uniqueness_theorem)란, 라플라스_방정식에 적절한 경계조건(boundary_condition)이 주어지면 퍼텐셜,potential을 하나의 값으로 완전히 정할 수 있다는 내용.
제 1 유일성 정리
제 2 유일성 정리 이렇게 있다는데 생략.
}
https://m.blog.naver.com/cindyvelyn/222051213345유일성정리(uniqueness_theorem)란, 라플라스_방정식에 적절한 경계조건(boundary_condition)이 주어지면 퍼텐셜,potential을 하나의 값으로 완전히 정할 수 있다는 내용.
제 1 유일성 정리
제 2 유일성 정리 이렇게 있다는데 생략.
}
이 방정식들은 (내 관점에서 현재는) 주로 전위,electric_potential#s-21.1 설명에 사용됨