Contents
- 1. 데과기
- 1.1. Week 1-1
- 1.2. Week 1-2
- 1.3. Week 2-1
- 1.4. Week 2-2
- 1.5. Week 3-1
- 1.6. Week 3-2
- 1.7. Week 4-2
- 1.8. week 5-1
- 1.9. week 5-2
- 1.10. week 6-1
- 1.11. week 6-2
- 1.12. week 7-1
- 1.13. week 7-2
- 1.14. Week 9-1
- 1.15. Week 9-2
- 1.16. Week 10-1
- 1.17. Week 10-2
- 1.18. Week 11-1
- 1.19. Week 11-2
- 1.20. Week 12-1
- 1.21. Week 12-2
- 1.22. Week 13-1
- 1.23. Week 13-2
- 1.24. Week 14-1
- 1.25. Week 14-2
1.1.1. linear algebra ¶
장점: compact representation을 가능하게 해 줌. 예를 들어 선형회귀,linear_regression model with
의 경우 다음 첫 식을 두번째 식으로 간단하게 표현 가능.
 \right)^2)

In this course, we cover
• Vectors and matrices, their operations
• Span, linear independence, basis, dimension …
• Linear transformations
• Least squares problem
• ...
i.e.
벡터,vector, 행렬,matrix, their operations
생성,span, 선형독립,linear_independence(compare 선형종속,linear_dependence), 기저,basis, 차원,dimension, ...
선형변환,linear_transformation
 least_square
least_square
의 경우 다음 첫 식을 두번째 식으로 간단하게 표현 가능.
• Vectors and matrices, their operations
• Span, linear independence, basis, dimension …
• Linear transformations
• Least squares problem
• ...
i.e.
벡터,vector, 행렬,matrix, their operations
생성,span, 선형독립,linear_independence(compare 선형종속,linear_dependence), 기저,basis, 차원,dimension, ...
선형변환,linear_transformation
1.1.2. prob / stat ¶
In this course, we cover
• Random variables, probability distribution, expectation, variance
• Common distributions including Bernoulli, Binomial, Geometric,
Poisson, Exponential, Uniform, Gaussian distributions
• Joint and conditional distribution, independency, joint Gaussian
• Basic statistics, confidence interval, hypothesis test, t-test
• …
i.e.
확률변수,random_variable, 확률분포,probability_distribution, 기대값,expected_value, 분산,variance
베르누이_분포,Bernoulli_distribution, 이항분포,binomial_distribution, 기하분포,geometric_distribution, 푸아송_분포,Poisson_distribution, 지수분포,exponential_distribution, 고른분포,uniform_distribution, Gaussian distribution(=정규분포,normal_distribution)
결합확률분포,joint_probability_distribution, conditional_distribution, 독립성,independence, joint Gaussian
conditional_distribution, 독립성,independence, joint Gaussian
통계,statistics, 신뢰구간,confidence_interval, 가설검정,hypothesis_test, t-test
t-test
• Random variables, probability distribution, expectation, variance
• Common distributions including Bernoulli, Binomial, Geometric,
Poisson, Exponential, Uniform, Gaussian distributions
• Joint and conditional distribution, independency, joint Gaussian
• Basic statistics, confidence interval, hypothesis test, t-test
• …
i.e.
확률변수,random_variable, 확률분포,probability_distribution, 기대값,expected_value, 분산,variance
베르누이_분포,Bernoulli_distribution, 이항분포,binomial_distribution, 기하분포,geometric_distribution, 푸아송_분포,Poisson_distribution, 지수분포,exponential_distribution, 고른분포,uniform_distribution, Gaussian distribution(=정규분포,normal_distribution)
결합확률분포,joint_probability_distribution,
통계,statistics, 신뢰구간,confidence_interval, 가설검정,hypothesis_test,
1.1.3. multivariable calculus and optimization ¶
In statistics or machine learning, mostly interested in finding models to explain the data
Optimization helps fit machine learning models on the data by choosing the parameters that either maximize or minimize a function like, for example,
• Likelihood of the data // 가능도,likelihood
• Loss function // 손실함수,loss_function
• Error obtained by the model on the (training) data // 오류,error? 오차,error?
• …
Optimization helps fit machine learning models on the data by choosing the parameters that either maximize or minimize a function like, for example,
• Likelihood of the data // 가능도,likelihood
• Loss function // 손실함수,loss_function
• Error obtained by the model on the (training) data // 오류,error? 오차,error?
• …
In this course, we cover
• Introduction to mathematical programming modeling
• Linear programming and duality // linear_programming 쌍대성,duality
linear_programming 쌍대성,duality
• Basics of multivariable calculus: derivatives, gradient, Hessian // 미분,derivative, 기울기,gradient, Hessian
Hessian
• Convex set and function // convex_set and 볼록함수,convex_function
convex_set and 볼록함수,convex_function
• Nonlinear programming, Lagrangian relaxation and KKT conditions
• Numerical optimization algorithms: gradient and Newton’s algorithms // 뉴턴_방법,Newton_method?
• …
• Introduction to mathematical programming modeling
• Linear programming and duality //
• Basics of multivariable calculus: derivatives, gradient, Hessian // 미분,derivative, 기울기,gradient,
• Convex set and function //
• Nonlinear programming, Lagrangian relaxation and KKT conditions
• Numerical optimization algorithms: gradient and Newton’s algorithms // 뉴턴_방법,Newton_method?
• …
1.3. Week 2-1 ¶
선형방정식,linear_equation
연립일차방정식,system_of_linear_equations
항등행렬,identity_matrix - curr at 단위행렬,unit_matrix
{
Diagonal entries가 모두 1이고 나머지가 모두 0인 정사각행렬,square_matrix.
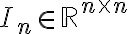
이것은 (행렬에 곱하기 뿐만 아니라) 벡터,vector에 (QQQ 우측에만?) 곱해도 그 벡터를 유지(preserve).
An identity matrix preserves any vector
preserves any vector 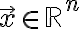 after multiplying
after multiplying 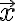 by
by 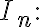

}
역행렬,inverse_matrix
역행렬이 존재하지 않으면? 그 선형방정식계는 해가 없거나 무한히 많은 해가 있다.
선형방정식계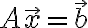 에서,
에서,  가 정사각행렬이 아닌 직사각행렬이라면?
가 정사각행렬이 아닌 직사각행렬이라면? )
방정식,equation의 수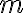 과 변수,variable의 수
과 변수,variable의 수  에 대해:
에 대해:
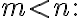 변수의 수가 더 많음 : 대개, 무한히 많은 해가 있다 - under-determined system
변수의 수가 더 많음 : 대개, 무한히 많은 해가 있다 - under-determined system
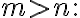 방정식의 수가 더 많음 : 대개, 해가 없다 - over-determined system
방정식의 수가 더 많음 : 대개, 해가 없다 - over-determined system
연립일차방정식,system_of_linear_equations
항등행렬,identity_matrix - curr at 단위행렬,unit_matrix
{
Diagonal entries가 모두 1이고 나머지가 모두 0인 정사각행렬,square_matrix.
An identity matrix
역행렬,inverse_matrix
역행렬이 존재하지 않으면? 그 선형방정식계는 해가 없거나 무한히 많은 해가 있다.
선형방정식계
방정식,equation의 수
1.4. Week 2-2 ¶
선형결합,linear_combination (of vectors) - 가중값,weight 혹은 계수,coefficient로
벡터방정식 form (아래)
생성,span
벡터방정식 해의 보장 조건:
벡터방정식
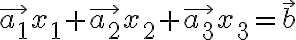
의 해는 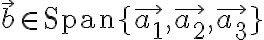 일때만 존재.
일때만 존재.
벡터방정식 form (아래)
생성,span
벡터방정식 해의 보장 조건:
벡터방정식
Matrix multiplications as Column Combinations
열,column들의 선형결합.
One column on the right
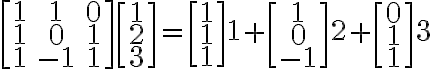
Multi-columns on the right
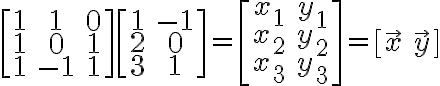
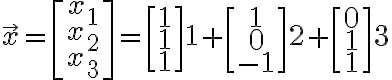
+\begin{bmatrix}1\\0\\-1\end{bmatrix}0+\begin{bmatrix}0\\1\\1\end{bmatrix}1)
행렬이 왼쪽에, 벡터가 오른쪽에, 이렇게 곱하는 것은 벡터의 열column들을 하나하나씩....? chk
(생략)
행렬이 왼쪽에, 벡터가 오른쪽에, 이렇게 곱하는 것은 벡터의 행row들과 ..? chk
열,column들의 선형결합.
One column on the right
벡터 자리에 행렬이 온다면, 그것들도 열column별로...? chk
Matrix multiplications as Row Combinations(생략)
행렬이 왼쪽에, 벡터가 오른쪽에, 이렇게 곱하는 것은 벡터의 행row들과 ..? chk
벡터 자리에 행렬이 온다면, 그것들도 행row별로....? chk
1.5. Week 3-1 ¶
// 강의자료 Week 3-1 p3 Recall: Linear System
다음 선형계,linear_system의
행렬방정식,matrix_equation 표현:
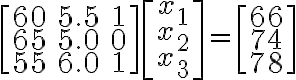
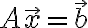
벡터방정식,vector_equation 표현:

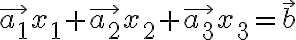
다음 선형계,linear_system의
| Person ID | Weight | Height | Is_smoking | Life-span |
| 1 | 60kg | 5.5ft | Yes(=1) | 66 |
| 2 | 65kg | 5.0ft | No(=0) | 74 |
| 3 | 55kg | 6.0ft | Yes(=1) | 78 |
행렬방정식,matrix_equation 표현:
해는 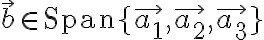 일 때만 존재한다.
일 때만 존재한다.
에 대한 해가 존재한다면, 언제 유일한가?
셋이 선형독립,linear_independence일 때 유일하다.
셋이 선형종속,linear_dependence이면 무한히 많은 해가 존재한다.
// p5 Linear Independence
(Practical) Definition:
(Practical) Definition:
Given a set of vectors 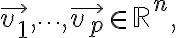
check if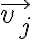 can be represented as a linear combination of the previous vectors
can be represented as a linear combination of the previous vectors 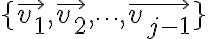 for
for 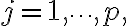
e.g.
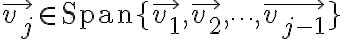 for some
for some 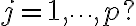
check if
e.g.
- If at least one such
is found, then
is linearly dependent.
- If no such
is found, then
is linearly_independent.
// p6 Linear Independence
(Formal) Definition:
(Formal) Definition:
Consider 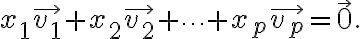
Obviously, one solution is
Obviously, one solution is
which we call a trivial solution.
are linearly independent if this is the only solution.
are linearly dependent if this system also has other nontrivial solutions,
e.g. at least onebeing nonzero.
// 두 정의는 동등하다.
만약 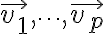 이것들이 선형종속이라면, 비자명해를 고려해본다.
이것들이 선형종속이라면, 비자명해를 고려해본다.
In the solution, let's denote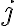 as the last index such that
as the last index such that 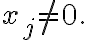
Then, one can write
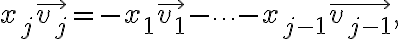
and safely divide it by  resulting in
resulting in
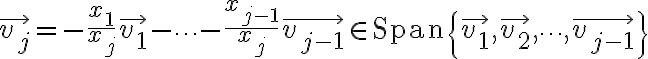
which means 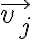 can be represented as a linear combination of the previous vectors.
can be represented as a linear combination of the previous vectors.
In the solution, let's denote
Then, one can write
1.7. Week 4-2 ¶
// 여기엔 임시로. 나중에 최소제곱,least_square으로 mv. //
원래
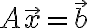
식이 성립하는 것이 이상적인 상황(?) 하지만 x값이 완전하지 않아서 오차,error를 만들기 때문에 이렇게 부등호가 붙는다.
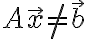
우리 목표는 최대한 근사,approximation하는 것이다. 이렇게.
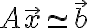
그리고 여기서 오차(errors - 벡터이므로 복수형?)는
 이다.
이다.
Now, the SSE - sum_of_squared_error s:

Definition.
Given an overdetermined system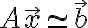
where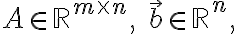 and
and 
a least_squares solution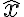 is defined as
is defined as
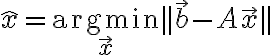
즉 error_vector 의 노름,norm을 최소화하는 x를 조심스럽게 선택하는 것이 목표.
Given an overdetermined system
where
a least_squares solution
- 이 least-squares problem에서 가장 중요한 측면(aspect)은, 어떤
를 선택하느냐에 상관없이, 벡터
will necessarily be in the 열공간,column_space
- Thus, we seek for
that makes
as the closest point in
to
1.15. Week 9-2 ¶
조건부,conditional
조건부확률,conditional_probability
조건부확률분포,conditional_probability_distribution
{
// 데과기 Week 9-2 p2
조건부확률질량함수,conditional_probability_mass_function,conditional_PMF
조건부확률밀도함수,conditional_probability_density_function,conditional_PDF
베이즈_정리,Bayes_theorem
{
// 데과기 Week 9-2 p3
)
}{P_Y(y)})
(여기에=\frac{P_{X,Y}(x,y)}{P_X(x)}) 즉
즉 =P_{Y|X}(y|x)P_X(x)) 를 적용하면)
를 적용하면)
P_X(x)}{P_Y(y)})
(여기에=\sum_u P_{X,Y}(u,y)=\sum_u P_{Y|X}(y|u) P_X(u)) 를 적용하면)
를 적용하면)
P_X(x)}{\sum_u P_{Y|X}(y|u) P_X(u)})
)
}{f_Y(y)})
f_X(x)}{f_Y(y)})
f_X(x)}{\int f_{Y|X}(y|u) f_X(u) du})
}
조건부기대값,conditional_expected_value
{
// 데과기 Week 9-2 p4
![$\text{E}[X|Y=y]$ $\text{E}[X|Y=y]$](/123/cgi-bin/mimetex.cgi?\Large \text{E}[X|Y=y])
)
or
dx)
}
조건부분산,conditional_variance
{
// 데과기 Week 9-2 p4
![$\text{Var}[X|Y=y]$ $\text{Var}[X|Y=y]$](/123/cgi-bin/mimetex.cgi?\Large \text{Var}[X|Y=y])
![$=\text{E}[(X-\text{E}[X|Y=y])^2|Y=y]$ $=\text{E}[(X-\text{E}[X|Y=y])^2|Y=y]$](/123/cgi-bin/mimetex.cgi?\Large =\text{E}[(X-\text{E}[X|Y=y])^2|Y=y])
![$=\text{E}[X^2|Y=y]-\text{E}[X|Y=y]^2$ $=\text{E}[X^2|Y=y]-\text{E}[X|Y=y]^2$](/123/cgi-bin/mimetex.cgi?\Large =\text{E}[X^2|Y=y]-\text{E}[X|Y=y]^2)
}
조건부확률,conditional_probability
조건부확률분포,conditional_probability_distribution
{
// 데과기 Week 9-2 p2
: conditional random variable
given
/// ... (처음 봤을때 잠깐 모호했는데,
라는 게 아니라
를 뜻한다)
Random event ofwhen
is determined as
- Conditional PMF and PDF
// conditional pdf = joint pdf / marginal pdf
조건부확률질량함수,conditional_probability_mass_function,conditional_PMF
조건부확률밀도함수,conditional_probability_density_function,conditional_PDF
베이즈_정리,Bayes_theorem
{
// 데과기 Week 9-2 p3
(여기에
(여기에
조건부기대값,conditional_expected_value
{
// 데과기 Week 9-2 p4
or
조건부분산,conditional_variance
{
// 데과기 Week 9-2 p4
Example: when =c) for
for 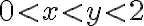 and
and 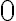 otherwise, find
otherwise, find ![$c,\;f_{X|Y}(x|y),\;\text{E}[X|Y=y]$ $c,\;f_{X|Y}(x|y),\;\text{E}[X|Y=y]$](/123/cgi-bin/mimetex.cgi?\Large c,\;f_{X|Y}(x|y),\;\text{E}[X|Y=y])
p6부터계속
확률변수의 독립: See 확률변수,random_variable#s-2 and 독립성,independence#s-3
X와 Y가 독립이면 X와 Y는 상관 관계가 없다.
하지만 역은 성립하지 않는다.
상관관계가 없다고 독립인 것은 아니다.
X와 Y가 독립이면 X와 Y는 상관 관계가 없다.
하지만 역은 성립하지 않는다.
상관관계가 없다고 독립인 것은 아니다.
joint Gaussian (normal) distribution - 결합,joint 정규분포,normal_distribution - 결합정규분포,joint_normal_distribution
식이 복잡해서 생략, 3차원 종 모양.
See Multivariate_normal_distribution
Multivariate_normal_distribution  multivariate normal distribution
multivariate normal distribution
각각의 marginal도 Gaussian. (i.e. 대충, 종 모양 곡면surface을 두(? 정확히) 평면에서 보면, 종 모양 곡선curve이 나타나는)
성질. X와 Y가 joint Gaussian이면,
식이 복잡해서 생략, 3차원 종 모양.
See
각각의 marginal도 Gaussian. (i.e. 대충, 종 모양 곡면surface을 두(? 정확히) 평면에서 보면, 종 모양 곡선curve이 나타나는)
성질. X와 Y가 joint Gaussian이면,
- X도 Y도 Gaussian; 하지만 역은 참이 아님.
X ~ N(…) and Y ~ N(…)
- conditional도 Gaussian. X|Y의 경우 평균은 x, y에 모두 영향을 받는데 분산은 y에 무관.
X|Y = y ~ N((여기 평균 부분에: y에 대한 식이 있음), (여기 분산 부분은: y의 값에 무관))
- X와 Y의 선형결합 즉 aX+bY도 Gaussian.
aX+bY ~ N(…)
- X와 Y가 독립 iff 둘의 (공분산,covariance이 0, 또는 '상관관계가 없음')
X ⊥ Y ↔ σX,Y=0
보통 화살표에서 → 부분은 참이지만 ← 부분은 항상 참이 아니다. 하지만 joint Gaussian일 경우 역도 참이 된다.
즉, joint Gaussian일 때는 독립성과 무상관관계가 동일하다. 이것은 Gaussian이 인기가 있는 이유 중 하나라고.
1.16. Week 10-1 ¶
random_sampling (kms: 임의추출, 확률추출)
random_sample (kms: 확률표본, 임의표본)
표본평균,sample_mean X̅
true_variance = 모분산,population_variance σ2
표본분산,sample_variance S2
표본표준편차,sample_standard_deviation
신뢰구간,confidence_interval p7
{
표본평균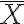 의 경우,
의 경우,
![$\text{Var}[\bar{X}]=\frac{\sigma^2}{n}$ $\text{Var}[\bar{X}]=\frac{\sigma^2}{n}$](/123/cgi-bin/mimetex.cgi?\Large \text{Var}[\bar{X}]=\frac{\sigma^2}{n}) 여야 하는데
여야 하는데
그런데 실제 분산(true variance = 모분산)을 알 방법이 없으므로, 대신 추정된 표본분산으로 추정한다.
![$\text{Var}[\bar{X}]=\frac{S^2}{n}$ $\text{Var}[\bar{X}]=\frac{S^2}{n}$](/123/cgi-bin/mimetex.cgi?\Large \text{Var}[\bar{X}]=\frac{S^2}{n})
random_sample (kms: 확률표본, 임의표본)
-  i.i.d. RVs from the same population.
i.i.d. RVs from the same population.
- 같은 모집단,population에서 온 iid 확률변수,random_variables들.
표본,sample
통계량,statistic- 같은 모집단,population에서 온 iid 확률변수,random_variables들.
표본,sample
A statistic is a value calculated from the observed random samples to say something about the whole population.
관찰된 random_samples에서 계산된 값 - whole population에 대해 말하기 위해서.
여기서 something은 보통 mean이나 average. - 평균,mean,average
true_mean = 모평균,population_mean관찰된 random_samples에서 계산된 값 - whole population에 대해 말하기 위해서.
여기서 something은 보통 mean이나 average. - 평균,mean,average
표본평균,sample_mean X̅
true_variance = 모분산,population_variance σ2
표본분산,sample_variance S2
표본표준편차,sample_standard_deviation
신뢰구간,confidence_interval p7
{
- Confidence in how close the sample mean is to the population mean
표본평균,sample_mean이 얼마나 모평균,population_mean에 가까운지에 대한 'confidence'. (신뢰도? 확신도? 확신하는 정도?)
- Depends on the sample size (𝑛) and standard deviation of the population (𝜎)
표본크기 sample_size과 모표준편차,population_standard_deviation
에 의존.
- If standard deviation of the population is unknown, will use the sample standard deviation
모표준편차를 모른다면, 표본표준편차를 사용.
- Estimated standard error is
표준오차(위에서 표본표준편차,sample_standard_deviation와 같다고..)는으로 추정함.
표본평균
그런데 실제 분산(true variance = 모분산)을 알 방법이 없으므로, 대신 추정된 표본분산으로 추정한다.
The sample mean is a common estimator of the true mean.
우리가 관심있는 건 확률이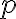 인 신뢰구간 - (p×100)% confidence interval
인 신뢰구간 - (p×100)% confidence interval
![$p=\text{Pr}\left[\bar{X}-k\frac{s}{\sqrt{n}} < \mu < \bar{X} + k\frac{s}{\sqrt{n}} \right] = \text{Pr}\left[ -k < \frac{\bar{X}-\mu}{\frac{S}{\sqrt{n}}} < k\right]$ $p=\text{Pr}\left[\bar{X}-k\frac{s}{\sqrt{n}} < \mu < \bar{X} + k\frac{s}{\sqrt{n}} \right] = \text{Pr}\left[ -k < \frac{\bar{X}-\mu}{\frac{S}{\sqrt{n}}} < k\right]$](/123/cgi-bin/mimetex.cgi?\Large p=\text{Pr}\left[\bar{X}-k\frac{s}{\sqrt{n}} < \mu < \bar{X} + k\frac{s}{\sqrt{n}} \right] = \text{Pr}\left[ -k < \frac{\bar{X}-\mu}{\frac{S}{\sqrt{n}}} < k\right])
True mean(모평균)이 이 구간,interval 안에 들어 있을 확률,probability은 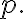
다시 말해 위 식을 한번 더 해석해보면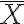 가 range [X̅ − k·SE[X̅], X̅ + k·SE[X̅]] 사이에 있을 확률이 p라는 얘기. (SD = SE는 standard deviation = standard error)
가 range [X̅ − k·SE[X̅], X̅ + k·SE[X̅]] 사이에 있을 확률이 p라는 얘기. (SD = SE는 standard deviation = standard error)
By the 중심극한정리,central_limit_theorem,CLT,
)
(바로 위에서 한 가정: X̅는 iid인 여러 확률변수들의 합. 식으로 나타내면 →) )
우리가 관심있는 건 확률이
다시 말해 위 식을 한번 더 해석해보면
By the 중심극한정리,central_limit_theorem,CLT,
t분포,t-distribution가 이를 위해 개발된 것.
t분포는
1.17. Week 10-2 ¶
가설검정,hypothesis_test
귀무가설,null_hypothesis
영분포 null_distribution
귀무가설,null_hypothesis
영분포 null_distribution
영가설(귀무가설)이 참일 때 모집단? 전체집단? 의 분포
a distribution of the whole population when the null hypothesis is true
대립가설,alternative_hypothesisa distribution of the whole population when the null hypothesis is true
오류,error
type_1_error
 유의_확률
유의_확률
그것과 p값을 비교하는 것이다.
(이하 단측검정만 고려한 서술)
type_1_error
null hypothesis가 사실 참인데, 기각해버리는 오류.
Type 1 error의 확률 =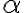 = level of significance. // 유의수준,significance_level (자막에선 '중요도 수준')
= level of significance. // 유의수준,significance_level (자막에선 '중요도 수준')
p값,p-value = 유의확률,significance_probability - Type 1 error의 확률 =
보통 1% level, 5% level and 10% level을 사용함.
Significance level이 높으면, type I error의 확률도 커짐.(자막) 영분포,null_distribution에서 관측 값을 초과하는 통계량,statistic이 나올 확률 - CHK
the probability that a statistic exceeding the observed one (toward the alternative hypothesis) is from the null distribution
(from other source) 귀무가설이 맞다고 가정하고 얻는 (가상의?) 결과보다, 극단적인 결과가 (실제로) 관측될 확률.
유의수준,significance_level을 정해 놓고 (보통 5% = 0.05)the probability that a statistic exceeding the observed one (toward the alternative hypothesis) is from the null distribution
(from other source) 귀무가설이 맞다고 가정하고 얻는 (가상의?) 결과보다, 극단적인 결과가 (실제로) 관측될 확률.
그것과 p값을 비교하는 것이다.
(이하 단측검정만 고려한 서술)
이하 두 줄 not sure; chk, 정확히.
p 값이 낮으면/작으면 - 영분포를 따른다는 가정 하에(영가설이 맞다는 가정 하에) - 그걸 벗어나는 극단적인 경우가 충분히 있음 significant - 영가설을 거부/기각. and 대립가설을 채택.
p 값이 높으면/크면 - 영분포를 따른다는 가정 하에(영가설이 맞다는 가정 하에) - 그걸 벗어나는 극단적인 경우가 충분하지 않음 not significant - 귀무가설을 기각하지 않음. (and 대립가설을 기각?)
암튼 확실한 것은
유의수준,significance_level의 값과 p값,p-value을 비교해서
p값이 작다 - 귀무가설을 기각
p값이 크다 - 귀무가설을 기각하지 않음
p 값이 낮으면/작으면 - 영분포를 따른다는 가정 하에(영가설이 맞다는 가정 하에) - 그걸 벗어나는 극단적인 경우가 충분히 있음 significant - 영가설을 거부/기각. and 대립가설을 채택.
p 값이 높으면/크면 - 영분포를 따른다는 가정 하에(영가설이 맞다는 가정 하에) - 그걸 벗어나는 극단적인 경우가 충분하지 않음 not significant - 귀무가설을 기각하지 않음. (and 대립가설을 기각?)
암튼 확실한 것은
유의수준,significance_level의 값과 p값,p-value을 비교해서
p값이 작다 - 귀무가설을 기각
p값이 크다 - 귀무가설을 기각하지 않음
생각: p값이 단순히 작다 크다로 생각하면 헷갈리고, 거기에 추가해 얼마나 deviate되었느냐(얼마나 significant한가)로 생각해야 덜 헷갈리는 듯?
1.19. Week 11-2 ¶
p4
최적화 모형의 구성요소 네 가지
모든 제약식(제약,constraint 식,expression)들을 만족하는
의사결정변수(결정변수,decision_variable)값 들 중에서
목적함수,objective_function를 최대화 혹은 최소화하는 의사결정변수 값을 결정한다.
- 결정변수,decision_variable
Controllable variables (decision maker가 제어 가능)
- 목적함수,objective_function (of the decision variables)
Measure(s) to evaluate system performance
- 제약,constraint
Restrictions on the decision variables
Restricted by business or physical rules - 예를 들어 생산량은 반드시 0 혹은 그 이상
- 매개변수,parameter
Uncontrollable variables - 제어할 수 없음
최적화에서 매개변수란, 일반적으로 수리계획법 모델 상에서의 상수값들을 뜻한다.
(반면, 통계 혹은 머신러닝에서 매개변수란 그 모형의 일부 수치적 특성을 뜻한다. 예를 들어 정규분포,normal_distribution는 평균 μ와 표준편차 σ로 특징지어지는데, 이 μ와 σ가 바로 매개변수.)
모든 제약식(제약,constraint 식,expression)들을 만족하는
의사결정변수(결정변수,decision_variable)값 들 중에서
목적함수,objective_function를 최대화 혹은 최소화하는 의사결정변수 값을 결정한다.
p6
그리고 제약 함수 constraint_function 들이 있다, 예를 들어
그럴 때,
Find
p7
feasible solution - 자막에선 '실행가능해'로 번역 ... 해,solution
) 이 모든 제약조건을 만족.
이 모든 제약조건을 만족.
feasible set

set of all feasible solutions
optimal solution feasible solution임과 동시에,
 \le f(\bar{x})) for every feasible solution
for every feasible solution 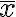 for minimization problem // minimization_problem
for minimization problem // minimization_problem
p8
선형함수,linear_function
(여기서 말하는) 선형함수는 a 다항식,polynomial of degree one or less
그리고 그 그래프는 직선straight_line.
(여기서 말하는) 선형함수는 a 다항식,polynomial of degree one or less
그리고 그 그래프는 직선straight_line.
p9
수리계획법에는 다양한 모형들이 있지만, 본 과목에선 다음 세 가지 유형에 대해서만 다룬다.
정수계획법(IP)은 선형계획법(LP)과 거의 같은데 차이는
정수계획법(IP)은 선형계획법(LP)과 거의 같은데 차이는
- LP : 모든 결정변수값이 실수,real_number.
- IP : 모든 또는 일부 결정변수값이 정수,integer.
p10
비선형계획법의 예 examples of non-linear programming
quadratic programming
Minimize
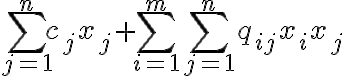
subject to
)
)
2차 계획법: 두 결정변수의 곱 ) 으로 되어 있다는 의미.
으로 되어 있다는 의미.
Minimize
quadratic constrained programming
Minimize
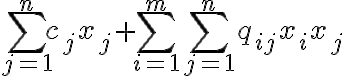
subject to
)
)
2차 제약조건 계획법: 목적함수 및 제약식 내 함수들이 모두 2차식인 경우. (quadratic objective and quadratic constraints)
Minimize
p11
제약,constraint의 세 유형
- less-than (≤) constraints
자원resources이나 용량capacities의 가용성availability을 표현
(e.g.) Number of products in production ≤ production capacity
ex. 생산중인 제품 수 ≤ production capacity (생산최대량?)
자막 - '생산량은 생산용량보다 작거나 같다'같이 나타낼 수 있는데 이는 생산용량보다 많이 생산을 할 수 없기 때문.
- greater-than (≥) constraints
문턱threshold이나 commitments를 표현
자막 - 충족시켜야 하는 한계점 혹은 일종의 약속 등을 나타낸다.
(e.g.) Number of products produced ≥ number of products ordered
ex. 생산된 제품 수 ≥ 주문받은 제품 수
자막 - '생산량은 주문량보다 크거나 같다'로 표현할 수 있는데, 이는 수요를 만족시키기 위해서는 수요량 이상 생산이 이루어져야 하기 때문.
- equal-to (=) constraints
balance나 consistency를 표현
자막 - 균형 또는 일관성을 나타냄
(e.g.) Products manufactured + products purchased = products in stock
자막 - '(생산량 + 구매량)은 현 재고량과 같다'고 나타낼 수 있다
p12
2차함수quadratic_function가 있을 때 최적화


(그림 왼쪽)
여기서 의사결정변수(결정변수,decision_variable) :
이차함수(목적함수,objective_function)는^2+1)
그리고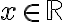 이고 그 외의 constraint는 없다.
이고 그 외의 constraint는 없다.
여기서 의사결정변수(결정변수,decision_variable) :
이차함수(목적함수,objective_function)는
그리고
(그림 오른쪽)
기계학습,machine_learning 기법 중 하나인 서포트벡터머신,support_vector_machine,SVM 기법을 수리계획법 모형으로 표현한 예시.
목적함수는 두 벡터의 곱 - 2차함수quadratic_function.
아랫줄은 제약조건.
SVM은 앞서 살펴본 비선형계획법 중 2차계획법 모형임을 알 수 있다.
기계학습,machine_learning 기법 중 하나인 서포트벡터머신,support_vector_machine,SVM 기법을 수리계획법 모형으로 표현한 예시.
목적함수는 두 벡터의 곱 - 2차함수quadratic_function.
아랫줄은 제약조건.
SVM은 앞서 살펴본 비선형계획법 중 2차계획법 모형임을 알 수 있다.
p13
선형회귀,linear_regression 예.
일반적으로 선형함수linear_function는
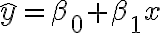
여기서
직선을 찾는다는 것은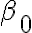 와
와 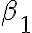 의 값을 찾는다는 것과 동일.
의 값을 찾는다는 것과 동일.
산점도 내 data points와 추정회귀선 사이 거리를 계산하는 방식은 다양 - 가로로(수평거리), 세로로(수직거리), 회귀선에 수직인 거리.
예측오차,prediction_error(예측,prediction 오차,error)는 위에서 두번째인 수직 거리.
Data point 중에서) 를 예로 들면, 오차 계산은 다음과 같이 한다.
를 예로 들면, 오차 계산은 다음과 같이 한다.
)
예측오차들의 합,sum을 근접성closeness을 평가하는 지표measure(측도,measure)로 활용할 수 있다.
추정회귀선보다 data point가 위에 있으면 양의 오차
추정회귀선보다 data point가 밑에 있으면 음의 오차
이것을 그냥 더하게 되면 서로 상쇄되어 예측오차들의 합을 과소평가하게 되는 상황이 발생 가능하므로 오차의 절대값,absolute_value이나 제곱,square을 사용.
일반적으로 선형함수linear_function는
직선을 찾는다는 것은
산점도 내 data points와 추정회귀선 사이 거리를 계산하는 방식은 다양 - 가로로(수평거리), 세로로(수직거리), 회귀선에 수직인 거리.
예측오차,prediction_error(예측,prediction 오차,error)는 위에서 두번째인 수직 거리.
Data point 중에서
추정회귀선보다 data point가 위에 있으면 양의 오차
추정회귀선보다 data point가 밑에 있으면 음의 오차
이것을 그냥 더하게 되면 서로 상쇄되어 예측오차들의 합을 과소평가하게 되는 상황이 발생 가능하므로 오차의 절대값,absolute_value이나 제곱,square을 사용.
1.20. Week 12-1 ¶
선형계획법,linear_programming - 수리계획법의 특별한 경우로,
공장 생산라인에서 P, Q를 각각 몇개 생산해야 하는가
 product-mix.problem
product-mix.problem
- 단일 목적함수
- 제약 식 함수가 모두 선형
- 모든 결정변수가 실수
- <, > 안됨. ≤ ≥ = 만 됨.
공장 생산라인에서 P, Q를 각각 몇개 생산해야 하는가
LP Example 2 - Diet Problem - 1930-40년대 최초의 LP 응용 사례
최소 비용으로 꼭 필요한 영양분nutrient을 충족시키려면 어떤 음식들을 사야 하는가
 diet.problem
diet.problem
최소 비용으로 꼭 필요한 영양분nutrient을 충족시키려면 어떤 음식들을 사야 하는가
1.21. Week 12-2 ¶
// Motivation
어떤 feasible_solution을 찾았다. objective_function 값이 124인. 그런데 최적의optimal objective_function 값은 모른다.
이 상황에서 최적값이 가질 수 있는 상한값 150을 누군가 찾았다. - 여기서 알 수 있는 것은 최적값이 124와 150 사이에 있다는 것.
이 상황에서 최적값의 상한값 142를 누군가 찾았다. - 상한값이 updated - 최적값은 124와 142 사이에 있다.
그 다음에 최적값의 상한값이 124임을 누군가 찾았다. - 최적값이 바로 124임을 찾았다.
따라서 최대화,maximization 문제에서는 최대한 낮은 상한값upper_bound 정보를 찾는 것이 중요하다.
(maybe rel. 해석학에서 상계,upper_bound. 그리고 최저의 상한값 = 최소상계 = least upper bound = lub = 상한,supremum)
어떤 feasible_solution을 찾았다. objective_function 값이 124인. 그런데 최적의optimal objective_function 값은 모른다.
이 상황에서 최적값이 가질 수 있는 상한값 150을 누군가 찾았다. - 여기서 알 수 있는 것은 최적값이 124와 150 사이에 있다는 것.
이 상황에서 최적값의 상한값 142를 누군가 찾았다. - 상한값이 updated - 최적값은 124와 142 사이에 있다.
그 다음에 최적값의 상한값이 124임을 누군가 찾았다. - 최적값이 바로 124임을 찾았다.
따라서 최대화,maximization 문제에서는 최대한 낮은 상한값upper_bound 정보를 찾는 것이 중요하다.
(maybe rel. 해석학에서 상계,upper_bound. 그리고 최저의 상한값 = 최소상계 = least upper bound = lub = 상한,supremum)
이하 부등식들을 조작하여 UB(upper bound)를 줄여가는 예제,
duality 설명,
duality theorems: 대충,
duality 설명,
duality theorems: 대충,
- weak_duality - 부등식이 성립하는
- strong_duality - 등식이 성립하는
- complementary_slackness
- 원 문제의 제약과 연관된 쌍대변수 값이 0이 아니면, 원 문제 제약은 등식을 만족해야
- 한 제약이 등식을 만족하지 않으면, 이 제약에 상응하는 쌍대변수는 0이어야
- 원 문제의 제약과 연관된 쌍대변수 값이 0이 아니면, 원 문제 제약은 등식을 만족해야
1.22. Week 13-1 ¶
The 2nd order (quadratic) approximation of  at
at 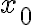 // quadratic_approximation
// quadratic_approximation
where
기울기,gradient
Suppose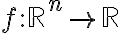
Gradient)
Suppose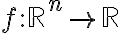
Suppose
Gradient
- A vector containing the partial derivatives of the function
at certain point
- 가장 가파른 상승steepest ascent의 방향,direction (i.e., 함수
의 최대 증가maximum increase) from
따라서,는 가장 가파른 하강steepest descent의 방향(최대 감소maximum decrease)
Suppose
- Matrix comprising the second-order partial derivatives of a function 𝑓
- Symmetric if 𝑓 is continuous // 연속성,continuity → 대칭행렬,symmetric_matrix
Suppose 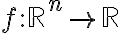 (다변수함수의 경우로 확장하면,)
(다변수함수의 경우로 확장하면,)
이렇게 gradient와 Hessian 등이 들어간다.
1.23. Week 13-2 ¶
볼록집합,convex_set
볼록성,convexity
A set of points 𝑋 is a convex set if every line segment joining two points of the set 𝑋 is entirely in the set.
A set is convex if
is convex if
y \in X)
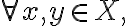 and
and ![$\forall t\in[0,1].$ $\forall t\in[0,1].$](/123/cgi-bin/mimetex.cgi?\Large \forall t\in[0,1].)
볼록성,convexity
A set of points 𝑋 is a convex set if every line segment joining two points of the set 𝑋 is entirely in the set.
A set
볼록집합의 성질
- X가 볼록이면, ∀a, {x+a|x∈X}도 볼록.
- X가 볼록이면, ∀a, {ax|x∈X}도 볼록.
- X와 Y가 볼록이면, X∩Y도 볼록.
볼록함수,convex_function
) is convex if
is convex if
x_2) \le tf(x_1)+(1-t) f(x_2))
for any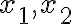 and
and ![$t\in[0,1]$ $t\in[0,1]$](/123/cgi-bin/mimetex.cgi?\Large t\in[0,1])
그래프에서는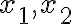 를 잇는 할선,secant_line(RHS)이 항상
를 잇는 할선,secant_line(RHS)이 항상 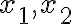 사이의 함수 그래프(LHS) 위에 있는.
사이의 함수 그래프(LHS) 위에 있는.
for any
그래프에서는
Convex function over  .....X 위로의 볼록함수?
.....X 위로의 볼록함수?
) is convex over
is convex over  if
if
x_2) \le tf(x_1)+(1-t) f(x_2))
for any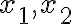
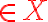 and
and ![$t\in[0,1]$ $t\in[0,1]$](/123/cgi-bin/mimetex.cgi?\Large t\in[0,1])
for any
...(some skips, tbw. or remove this line.)...
다변수함수 multivariable_function ) for
for 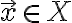 를 고려한다.
를 고려한다.
이것의 헤세_행렬,Hessian_matrix이 모든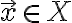 에 대해 존재한다면,
에 대해 존재한다면,
![[https]](/123/imgs/https.png) {{1,1},{1,1}} positive definite
{{1,1},{1,1}} positive definite
이것의 헤세_행렬,Hessian_matrix이 모든
is strictly convex over
if its Hessian matrix is positive definite for any
is convex over
if its Hessian matrix is positive semi-definite for any
is strictly concave over
if its Hessian matrix is negative definite for any
is concave over
if its Hessian matrix is negative semi-definite for any
![[https]](/123/imgs/https.png) {{1,1},{1,1}} positive definite
{{1,1},{1,1}} positive definitenxn행렬의 주소행렬식은
1st principal minor(s),
2nd principal minor(s), ...,
n-th principal minor 이렇게 있다.
이것들은 각각 1x1, 2x2, ..., nxn 행렬의 행렬식이다.
1st principal minor(s),
2nd principal minor(s), ...,
n-th principal minor 이렇게 있다.
이것들은 각각 1x1, 2x2, ..., nxn 행렬의 행렬식이다.
leading_principal_minor =,leading_principal_minor .
{
주 소행렬식중 특별히 '선도 주 소행렬식'이 있고 D_k 로 표기.
{
주 소행렬식중 특별히 '선도 주 소행렬식'이 있고 D_k 로 표기.
마지막 행과 열을 삭제하여 만드는.
// 데과기 13-2 35:50
The k-th leading principal minor of matrix H (denoted by D_k)
is the determinant of k×k matrix
obtained by deleting the last (n-k) rows and the last (n-k) columns of the matrix.
The k-th leading principal minor of matrix H (denoted by D_k)
is the determinant of k×k matrix
obtained by deleting the last (n-k) rows and the last (n-k) columns of the matrix.
// 38m
H가 n×n 대칭행렬,symmetric_matrix이라 하면,
} // principal_minor
H가 n×n 대칭행렬,symmetric_matrix이라 하면,
- H is positive definite iff
for all leading principal minors
- H is positive semi-definite iff
for all principal minors
- H is negative definite iff
for all leading principal minors
- H is negative semi-definite iff
for all principal minors
} // principal_minor
1.24. Week 14-1 ¶
Optima: Minima, Maxima
Sub:
국소 최적 - 국소최적,local_optimum
}local_minimum
local_maximum
전역 최적 - 전역최적,global_optimumlocal_maximum
global_minimum
global_maximum
global_maximum
Suppose:
feasible_set) 에서 실수
에서 실수 ) 로 가는 함수
로 가는 함수  를 가정.
를 가정.
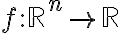
근방,neighborhood이란:
점 에 대해, 그 근방
에 대해, 그 근방 ) 은 다음과 같은 공,ball이다.
은 다음과 같은 공,ball이다.
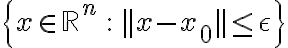
local_minimum:
feasible_set
점
어떤 근방 ) 안에서
안에서
모든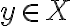 에 대해
에 대해
\le f(y)) 이면
이면
 의 local minimum이
의 local minimum이 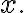
local_maximum: // (위와 부등호 방향만 반대)모든
어떤 근방 ) 안에서
안에서
모든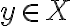 에 대해
에 대해
\ge f(y)) 이면
이면
 의 local maximum이
의 local maximum이 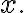
local_extremum (pl. local extrema)은 그것의 근방,neighborhood 안에서 최고의 해(best solution)이다.모든
(당연하지만)
global_minimum 은 local_minimum 들 중에서 찾는 것.
global_maximum 은 local_maximum 들 중에 있는 것.
global_minimum 은 local_minimum 들 중에서 찾는 것.
global_maximum 은 local_maximum 들 중에 있는 것.
Stationary Points and Local Optima
정류점,stationary_point (writing, 나중에 저기로 copy)
• For a single variable function 𝑓(𝑥), 𝑥0 is a stationary point if
기울기,slope = 0
기울기,gradient = 0 ? chk
𝑓′(𝑥0) = 0
• For a multi-variable function 𝑓(𝒙), 𝒙𝟎 is a stationary point if𝛻𝑓(𝒙𝟎) = 𝟎
각각기울기,slope = 0
기울기,gradient = 0 ? chk
• For a single variable function 𝑓(𝑥),
• Stationary point 𝑥0 with 𝑓′′(𝑥0) > 0 must be a local minimum
• Stationary point 𝑥0 with 𝑓′′(𝑥0) < 0 must be a local maximum
• For a multi-variable function 𝑓(𝒙), // 헤세_행렬,Hessian_matrix을 가지고 판별. 𝛻2는 라플라시안,Laplacian이 아니고 헤시안임.• Stationary point 𝑥0 with 𝑓′′(𝑥0) < 0 must be a local maximum
• Stationary point 𝒙𝟎 with positive definite 𝛻2𝑓(𝒙𝟎) must be a local minimum
• Stationary point 𝒙𝟎 with negative definite 𝛻2𝑓(𝒙𝟎) must be a local maximum
• Stationary point 𝒙𝟎 with negative definite 𝛻2𝑓(𝒙𝟎) must be a local maximum
Saddle Points
...
다음 constrained NLP를 생각
![$L(\vec{x},\vec{\lambda})=f(\vec{x})+\sum_{j=1}^k \lambda_j \left[ b_j - g_j(\vec{x}) \right]$ $L(\vec{x},\vec{\lambda})=f(\vec{x})+\sum_{j=1}^k \lambda_j \left[ b_j - g_j(\vec{x}) \right]$](/123/cgi-bin/mimetex.cgi?\Large L(\vec{x},\vec{\lambda})=f(\vec{x})+\sum_{j=1}^k \lambda_j \left[ b_j - g_j(\vec{x}) \right]) with
with 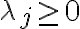 for
for 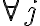
우변의 오른쪽의 시그마 항은 'penalty term'으로 해석된다.
Maximize )
Subject to \le b_j \;\;\;\text{for }\; j=1,2,\ldots,k)
그러면 NLP의 Lagrangian function은 이렇게 정의.Subject to
Karush-Kuhn-Tucker (KKT) Conditions
한 점 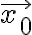 는 다음 네 가지가 만족하면 KKT조건을 만족하는 것.
는 다음 네 가지가 만족하면 KKT조건을 만족하는 것.
KKT조건을 만족한다고 해서 항상 최적인 것은 아님. (e.g. 안장점,saddle_point)
i.e.
- KKT조건은 NLP model에 대한 최적조건의 필수조건. - chk; 최적해의 필요조건,necessary_condition?
- optimum은 KKT 조건을 만족.

