Up: 수학,math
Sub:
미적분학의기본정리,FTC
극한,limit
극한_EpsilonDeltaLimitDefinition
MIT_Single_Variable_Calculus and MIT_Multivariable_Calculus
삼각함수_미분표
삼각함수_적분표
여러가지미분표와적분표
평균값정리,mean_value_theorem,MVT
롤_정리,Rolle_s_theorem
최대최소정리,extreme_value_theorem,EVT
중간값정리,사이값정리,intermediate_value_theorem,IVT
극값,extremum
임계점,critical_point
로피탈_정리,L_Hopital_s_rule
오목/볼록 오목볼록 - 밑에 임시 section 만듦. see below. 오목볼록,concave_and_convex
클레로_정리,Clairaut_theorem
이 둘은 page 필요? TBD
미분학,differential_calculus differential_calculus { 미분법 or 미분학 due to differential calculus
differential calculus
 differential_calculus
differential_calculus
differential calculus } // differential calculus
// 나중에 아래 section 3 (i.e. 미적분,calculus#s-3)과 합치는 거 고려
Sub:
noncommutative_differential_calculus // 이페이지아래언급
Boolean_differential_calculus // 불_대수,Boolean_algebra?action=highlight&value=Boolean_differential_calculus(맨 아래)에 언급
적분학,integral_calculus { '적분학' due to  integral calculus
integral calculus
// basic calculus(?)가 아닌, 레벨이/차원이/... 올라간
다변수미적분,multivariable_calculus
벡터미적분,vector_calculus - 벡터,vector
행렬미적분,matrix_calculus matrix_calculus - writing - rel. 행렬,matrix
텐서미적분,tensor_calculus tensor_calculus - writing - rel. 텐서,tensor
연산미적분,operational_calculus - writing - rel. 연산자,operator 연산,operation
극한,limit
극한_EpsilonDeltaLimitDefinition
MIT_Single_Variable_Calculus and MIT_Multivariable_Calculus
삼각함수_미분표
삼각함수_적분표
여러가지미분표와적분표
평균값정리,mean_value_theorem,MVT
롤_정리,Rolle_s_theorem
최대최소정리,extreme_value_theorem,EVT
중간값정리,사이값정리,intermediate_value_theorem,IVT
극값,extremum
임계점,critical_point
로피탈_정리,L_Hopital_s_rule
오목/볼록 오목볼록 - 밑에 임시 section 만듦. see below. 오목볼록,concave_and_convex
클레로_정리,Clairaut_theorem
이 둘은 page 필요? TBD
미분학,differential_calculus differential_calculus { 미분법 or 미분학 due to
differential calculus } // differential calculus
// 나중에 아래 section 3 (i.e. 미적분,calculus#s-3)과 합치는 거 고려
Sub:
noncommutative_differential_calculus // 이페이지아래언급
Boolean_differential_calculus // 불_대수,Boolean_algebra?action=highlight&value=Boolean_differential_calculus(맨 아래)에 언급
// basic calculus(?)가 아닌, 레벨이/차원이/... 올라간
다변수미적분,multivariable_calculus
벡터미적분,vector_calculus - 벡터,vector
행렬미적분,matrix_calculus matrix_calculus - writing - rel. 행렬,matrix
텐서미적분,tensor_calculus tensor_calculus - writing - rel. 텐서,tensor
연산미적분,operational_calculus - writing - rel. 연산자,operator 연산,operation
operational calculus
'연산계산법' via operational calculus ... but 저걸 찾으면 초등학교 계산(elementary arithmetic) 얘기만
operational calculus ... but 저걸 찾으면 초등학교 계산(elementary arithmetic) 얘기만
연산(자) 계산|미적분|미적
MKL umbral_calculus { umbral calculus umbral_calculus
umbral_calculus  UmbralCalculus
UmbralCalculus  Umbral_calculus
Umbral_calculus  음계산법
음계산법  陰計算 } // umbral calculus ...
陰計算 } // umbral calculus ...  umbral calculus
umbral calculus  umbral calculus
umbral calculus  umbral calculus
umbral calculus
tmp video { https://www.youtube.com/watch?v=N8Rxlc-fGr0 }
 operational_calculus
operational_calculus
 Operational_calculus
Operational_calculus
https://encyclopediaofmath.org/wiki/Operational_calculus
// operational calculus .... operational calculus
operational calculus  operational calculus
operational calculus  연산계산법
연산계산법
// 기타 단어가 -calculus지만 해석학/미적분과는 관계 없는 것들이 많은데... 일단은 맨 아래 기타 문단에'연산계산법' via
연산(자) 계산|미적분|미적
MKL umbral_calculus { umbral calculus
tmp video { https://www.youtube.com/watch?v=N8Rxlc-fGr0 }
https://encyclopediaofmath.org/wiki/Operational_calculus
// operational calculus ....
Contents
1. Links ¶
서울대 미적 기출문제 + 해답
http://www.math.snu.ac.kr/taoffice/calculus/QnA/QnA-033.005.html
KAIST 미적 기출문제
http://mathsci.kaist.ac.kr/home/resource/oldexam/
http://www.math.snu.ac.kr/taoffice/calculus/QnA/QnA-033.005.html
KAIST 미적 기출문제
http://mathsci.kaist.ac.kr/home/resource/oldexam/
tmp {
서울대 교양수학 홈페이지
http://www.math.snu.ac.kr/taoffice/calculus/syllabi/2014/index.html
http://www.math.snu.ac.kr/taoffice/calculus/syllabi/2014/first-semester/033.001-frame.html
}
서울대 교양수학 홈페이지
http://www.math.snu.ac.kr/taoffice/calculus/syllabi/2014/index.html
http://www.math.snu.ac.kr/taoffice/calculus/syllabi/2014/first-semester/033.001-frame.html
}
Videos
Dr. Bazett, Calculus III: Multivariable Calculus
https://www.youtube.com/playlist?list=PLHXZ9OQGMqxc_CvEy7xBKRQr6I214QJcd
Dr. Bazett, Calculus III: Multivariable Calculus
https://www.youtube.com/playlist?list=PLHXZ9OQGMqxc_CvEy7xBKRQr6I214QJcd
2. tmp buf ¶
역사적으로는, 겉보기에 전혀 다른 두 개념
- 곡선,curve으로 둘러싸인 영역의 넓이,area의 계산 (Archimedes)
- 움직이는 입자,particle의 순간 속도,velocity (Newton)
2.1.6. Courant ¶
Differential and integral calculus by Courant
Introduction to Calculus and Analysis by Courant and John (2-volume)
Introduction to Calculus and Analysis by Courant and John (2-volume)
2.1.7. Keisler ¶
Elementary Calculus
Elementary Calculus: An Infinitesimal Approach
On-line Edition. Copyright © 2000 by H. Jerome Keisler, revised December 2023.
https://people.math.wisc.edu/~hkeisler/calc.html
On-line Edition. Copyright © 2000 by H. Jerome Keisler, revised December 2023.
https://people.math.wisc.edu/~hkeisler/calc.html
온라인 공개, 25 MB pdf
3. 미분 ¶
단어_미분
{
Sub:
 미분 - 위의 것들 비교 설명 잘해놓음.
미분 - 위의 것들 비교 설명 잘해놓음.
}
{
Sub:
미분,derivative - 미분한 것, 미분한 결과, 도함수
미분,differentiation - 미분하는 행동, 미분하는 방법, 미분법(法)
미분,differential - 디퍼렌셜, 미분소(素) // tmp: goto 미분,differential
미분,differential
미분,differentiation - 미분하는 행동, 미분하는 방법, 미분법(法)
미분,differential - 디퍼렌셜, 미분소(素) // tmp: goto
}
미분이라고 번역되는 단어는 다양.
사전적 의미는
- differentiation
n. 구별, 차별; 미분
- differentiate
v. 구별하다
- differential
n. 차이, 격차
- derivative
n. 파생어, 파생물 (참고: derive v. 끌어내다, 얻다; (수학) 유도하다)
differentiation
derivative
함수 y=f(x)의 x=a에서 x=b(a≠b)까지의 평균변화율은,
미분(하는 행동)
the process of finding a derivative
differentiate해서 derivative를 얻는 과정
derivative를 찾는 것
differentiatethe process of finding a derivative
differentiate해서 derivative를 얻는 과정
derivative를 찾는 것
미분하다
도함수(derivative)를 얻다
differential도함수(derivative)를 얻다
derivative
미분한 것
순간변화율, 미분계수, 도함수
도함수라는 번역이 주로 쓰이지만 일본어번역투라서 유도함수로 써야 한다는 의견이 있음. (수갤)
differentiation의 결과
기본적인 개념은 변화율(rate of change, Δy/Δx 등으로 나타내는 그것, 관련 개념 비,ratio and 비율,rate)에서 왔다.순간변화율, 미분계수, 도함수
도함수라는 번역이 주로 쓰이지만 일본어번역투라서 유도함수로 써야 한다는 의견이 있음. (수갤)
differentiation의 결과
평균변화율 average rate of change
-f(a)}{h})
{함수 y=f(x)의 x=a에서 x=b(a≠b)까지의 평균변화율은,
(y의 증분)/(x의 증분)
-f(a)}{b-a})
이며, 이것은 두 점 (a,f(a))와 (b,f(b))를 지나는 직선의 기울기,slope와 같다.기타 관련 단어로는
antiderivative 역도함수
antidifferentiation
differentiable 미분가능(한)
differentiability 미분가능성 - 미분가능성,differentiability { differentiable 미분가능(한) adj. }
antiderivative 역도함수
antidifferentiation
differentiable 미분가능(한)
differentiability 미분가능성 - 미분가능성,differentiability { differentiable 미분가능(한) adj. }
연속하는continuous 연속continuation - 연속성,continuity
변곡점,inflection_point
cusp (두 곡선이 만나는 뾰족한) 끝 - is_a 점,point? always? chk
discontinuity 중단, 단절; 수학에선 불연속(성) - 불연속성,discontinuity
order 미분한 횟수. (미분방정식,differential_equation에서는 order와 degree를 잘 구분해야 함: order = 계수 = 최대 미분 횟수, degree = 차수 = 최대 order인 도함수를 몇번이나 제곱했는지)
변곡점,inflection_point
cusp (두 곡선이 만나는 뾰족한) 끝 - is_a 점,point? always? chk
discontinuity 중단, 단절; 수학에선 불연속(성) - 불연속성,discontinuity
order 미분한 횟수. (미분방정식,differential_equation에서는 order와 degree를 잘 구분해야 함: order = 계수 = 최대 미분 횟수, degree = 차수 = 최대 order인 도함수를 몇번이나 제곱했는지)
미분소
미분,differential.
differential의 뜻이 여럿 있는데 그 중 infinitesimal 관련을 뜻하는 듯. 미분소
미분소  Differential_(infinitesimal) ←
Differential_(infinitesimal) ←  Differential_(mathematics) ←
Differential_(mathematics) ←  Differential
Differential
무한소,infinitesimal와의 정확한 관계는 모르겠음. 무한소
무한소  Infinitesimal
Infinitesimal  무한소
무한소
Relateddifferential의 뜻이 여럿 있는데 그 중 infinitesimal 관련을 뜻하는 듯.
무한소,infinitesimal와의 정확한 관계는 모르겠음.
미적분학의기본정리,FTC에 의하면 antidifferentiation = integration
5. 미적분 기호 ¶
y를 x에 대해
Leibniz식은 독립변수와_종속변수를 각각 분모와 분자에 나타냄.
Lagrange notation은 prime notation이라고도 함.
| 미분 | 두번 미분 | n번 미분 | 적분 | |
| Lagrange | ||||
| Leibniz | ||||
| Newton | ? | ? | ||
| Euler | ? |
Leibniz식은 독립변수와_종속변수를 각각 분모와 분자에 나타냄.
Lagrange notation은 prime notation이라고도 함.
QQQQ Euler notation의 D가 미분연산자?? chk
| 표기법(notation) 이름 | example |
| Leibniz notation | |
| prime notation | |
| Newton's dot notation | |
| subscript notation |
from Zill 6e
CLEANUP:
미분기호
미분기호
| Lagrange's | Leibniz's |
| 이계도함수 | |
| 삼계도함수 | |
| N계도함수 |
6. tmp; 서강대 1학년 .. 임시로 퍼옴. 읽고 지울것 ¶
STS2005 미적분학 I
미적분학 I은 모든 자연과학대 학생과 공과대학 학생이 들어야 하는 필수 교양 과목이다. 수학으로의 첫 입문 과목이라고 할 만하다. 교재로는 Stewart 책을 사용한다.
미적분학 I에서 제일 큰 난관은 ϵ−δ증명법이라고 할 수 있다. 극한_EpsilonDeltaLimitDefinition엡실론-델타 논법이란 자연스럽게 받아들였던 함수의 극한 및 수열의 극한극한,limit을 엄밀하게 증명하는 방법이다. 기초적인 개념이 받아들이기 어렵기에 대체적으로 적용은 쉬운 기초적인 함수 등에 국한된다.
고등학교에서 당연하게 받아들였던 Rolle's Theorem롤_정리,Rolle_s_theorem, Mean Value Theorem평균값정리,mean_value_theorem,MVT 등을 증명해 본다. 그 후 고등학교에서 다루지 않았던 역삼각함수역삼각함수,inverse_trigonometric_function와 hyperbolic function쌍곡선함수,hyperbolic_function 등을 배운다. 그리고 이들을 미분하는 방법을 배운다.
적분의 경우에도 고등학교에서 배웠던 범위에서 확장된다. Δx가 균등하지 못한 Riemann Sum리만_합,Riemann_sum 등을 배운다. 그리고 우리가 배웠던 함수들의 부정적분부정적분,indefinite_integral을 구하는 방법과 미적분학의 기본 정리(FTC)미적분학의기본정리,FTC 등을 배운다. 그 후 수열수열,sequence에서 무한급수무한급수,infinite_series의 다양한 수렴 판정법수렴판정법,convergence_test을 배운다. 그리고 마지막으로 Taylor Series테일러_급수,Taylor_series에 관한 내용을 배우게 된다.
고등학교 미적분에 익숙하다면 일반적인 과목보다 A+ 성취 난이도가 높지 않은 편이다.
1.5STS2006 미적분학 II
미적분학 II는 미적분학 I에 이어지는 자과대생과 공대생을 위한 필수 과목이다. 우선 고등학교 때 배웠던 매개 변수 방정식매개변수방정식,parametric_equation에 대해 배운다. 매개 변수 방정식의 미적분을 하면서 이에 익숙해지게 된다. 그 후 배웠던 것을 극좌표,polar_coordinate라는 새로운 좌표계좌표계,coordinate_system를 도입하게 된다. 그리고 x와 y를 r과 θ에 관한 매개 변수 방정식으로 표현하는 법을 배운다. 그리고 미적분학 과목 답게 그에 관해 미적분을 한다. 이때 배우는 극좌표로 재미있는 도형들을 표현해보기도 한다.
매개 변수 방정식의 연장선상으로 공간에 와서 여러 벡터방정식벡터방정식,vector_equation을 다룬다. 직선직선,line과 곡선곡선,curve, 그리고 평면평면,plane의 벡터방정식을 다루게 된다. 벡터곱인 내적내적,inner_product과 외적외적,outer_product의 여러 성질들도 다룬다.
고등학교 때 배웠던 일변수 함수인 f(x)와 같은 함수에서 벗어나 이제 이변수 함수, 삼변수 함수인 f(x,y), f(x,y,z)에 관한 여러 성질들도 배운다. 극한극한,limit이 어떻게 정의되는지 다루는 과정에서 또다시 ϵ−δ논법극한_EpsilonDeltaLimitDefinition을 만난다. 이변수함수에서 등장하는 미분법인 편미분편미분,partial_derivative, 방향도함수방향도함수,directional_derivative, gradient 벡터기울기벡터,gradient_vector 등을 배운다.
그리고 다변수함수의 적분을 함으로써 미적분학 II 과목이 끝나게 된다. 이중적분이중적분,double_integral, 삼중적분삼중적분,triple_integral 등을 반복적분(iterated_integral(s)? repeated_integral? multiple_integral?)으로 표현하는 방법을 배우고, 이때 구구,sphere 등을 더 편하게 적분할 수 있도록 원기둥 좌표계와 구면 좌표계 등을 배운다. 그 후 선적분선적분,line_integral에 대한 내용을 다룬 후 과목이 끝난다.
7. tmp; Knuth: epsilon-delta 설명의 대안? ¶
Knuth가 Cauchy의 엄밀한 epsilon-delta 대신 Big O notation을 사용하는 새로운 형태의 미적분학 교육을 제안했던 적이 있음
http://www.ams.org/notices/199806/commentary.pdf
http://www.ams.org/notices/199806/commentary.pdf
from 미적분학 교육에서 극한을 제거해야 하는가? https://zariski.wordpress.com/2012/06/04/미적분학-교육에서-극한을-제거해야-하는가/
비표준해석학인가?
9. tmp; 오목볼록 ¶
오목볼록 관련 내용 compilation. (2020-10-28)
분류는???
분류는???
단어정리
convex 볼록한 (콘벡스 컨벡스)
convexity 볼록함 볼록성 컨벡시티 철(凸) (기타: 볼록한 형태(모양)/곳/면)
concave 오목한
concavity 오목함 오목성 (칸캐버티) 요(凹) (기타: 오목한 형태(모양)/곳/면)
convexity 볼록함 볼록성 컨벡시티 철(凸) (기타: 볼록한 형태(모양)/곳/면)
concave 오목한
concavity 오목함 오목성 (칸캐버티) 요(凹) (기타: 오목한 형태(모양)/곳/면)
cf.
cavity는 뭔가의 속에 있는 구멍(이나 빈 부분, 공동)을 뜻하는데 관련있을듯.
cavity는 뭔가의 속에 있는 구멍(이나 빈 부분, 공동)을 뜻하는데 관련있을듯.
위로 볼록(concave down)
아래로 볼록(concave up)
아래로 볼록(concave up)
응용:
convex function 볼록함수 - 볼록함수,convex_function
convex set 볼록집합 - 볼록집합,convex_set
convex optimization 볼록최적화 - 볼록최적화,convex_optimization
concave function 오목함수 - 오목함수,concave_function
strictly convex 까다로운 볼록 - 정의 TBW
convex function 볼록함수 - 볼록함수,convex_function
convex set 볼록집합 - 볼록집합,convex_set
convex optimization 볼록최적화 - 볼록최적화,convex_optimization
concave function 오목함수 - 오목함수,concave_function
strictly convex 까다로운 볼록 - 정의 TBW
CHK
{
ref. S는 ℝ 위의 벡터공간,vector_space이라고 하고
Def: C⊂S인 집합 C가 다음을 만족하면 볼록 집합(convex set)으로 부른다.
![$\forall x,y\in C,\; \forall t\in [0,1]:$ $\forall x,y\in C,\; \forall t\in [0,1]:$](/123/cgi-bin/mimetex.cgi?\Large \forall x,y\in C,\; \forall t\in [0,1]:)
x+ty\in C)
Def: 함수 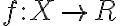 가 다음을 만족하면 볼록함수로 부른다.
가 다음을 만족하면 볼록함수로 부른다.
![$\forall x_1,x_2\in X,\; \forall t\in[0,1]:$ $\forall x_1,x_2\in X,\; \forall t\in[0,1]:$](/123/cgi-bin/mimetex.cgi?\Large \forall x_1,x_2\in X,\; \forall t\in[0,1]:)
x_2) \le tf(x_1)+(1-t)f(x_2))
(아래로 볼록, 위로 오목)
{
ref. S는 ℝ 위의 벡터공간,vector_space이라고 하고
Def: C⊂S인 집합 C가 다음을 만족하면 볼록 집합(convex set)으로 부른다.
Def: Jensen inequality - 옌센_부등식,Jensen_inequality
함수\to R) 가 연속인 볼록함수,convex_function라면, 다음을 만족.
가 연속인 볼록함수,convex_function라면, 다음을 만족.
,\; p_i>0,\; \sum_{i=1}^n p_i = 1)
 \le \sum_{i=1}^n p_i f(x_i))
증명은 수학적귀납법,mathematical_induction 사용. 해당 사이트에.
함수
이용: 평균,mean,average에서 산술평균 ≥ 기하평균 증명 등.
CHK
{
![$\forall x,y\in\mathbb{R},\,t\in[0,1]$ $\forall x,y\in\mathbb{R},\,t\in[0,1]$](/123/cgi-bin/mimetex.cgi?\Large \forall x,y\in\mathbb{R},\,t\in[0,1]) 에 대해 다음 식이 항상 성립하는 함수
에 대해 다음 식이 항상 성립하는 함수  가 볼록함수란다.
가 볼록함수란다.
y) \le tf(x)+(1-t)f(y))
concave function 오목함수 ..... 는 부호만? (그럼 위아래만?) (그럼 식의 부등호만?) 바꾸면 된다. 위로 볼록한 함수는 아래로는 ‘오목’한 함수니까.
}
![[https]](/123/imgs/https.png) src 기타 convexity를 보존하는 연산, convex function의 특성 언급.
src 기타 convexity를 보존하는 연산, convex function의 특성 언급.
{
}
![[https]](/123/imgs/https.png) src 기타 convexity를 보존하는 연산, convex function의 특성 언급.
src 기타 convexity를 보존하는 연산, convex function의 특성 언급.관련:
기타: (오목볼록 관련 주제들)
볼록집합,convex_set
볼록최적화,convex_optimization
볼록해석,convex_analysis
볼록공간,convex_space - writing
곡선의 오목과 볼록 (이건 고딩때부터..)
변곡점,inflection_point 에선 오목/볼록이 바뀜.
곡률,curvature
볼록껍질,convex_hull(kms 수학용어는 "볼록집합") 컨벡스 껍질(convex hull): 컨벡스 도형의 바깥을 구성하는 점의 집합?
기타: (오목볼록 관련 주제들)
볼록집합,convex_set
볼록최적화,convex_optimization
볼록해석,convex_analysis
볼록공간,convex_space - writing
곡선의 오목과 볼록 (이건 고딩때부터..)
변곡점,inflection_point 에선 오목/볼록이 바뀜.
곡률,curvature
볼록껍질,convex_hull(kms 수학용어는 "볼록집합") 컨벡스 껍질(convex hull): 컨벡스 도형의 바깥을 구성하는 점의 집합?
기울기하강,gradient_descent을 사용할 때, convex 함수(볼록함수,convex_function)와 non-convex 함수에서 탐색한 해,solution는 큰 차이를 갖는다.
tmp links ko about convexity:
https://hwiyong.tistory.com/7
https://hwiyong.tistory.com/8 (kmooc 요약) - 헤세_행렬,Hessian_matrix 언급.
https://hwiyong.tistory.com/7
https://hwiyong.tistory.com/8 (kmooc 요약) - 헤세_행렬,Hessian_matrix 언급.
misc
오목볼록에는) 의 선형결합이 나오는데 vector equation of a line(직선,line의 벡터방정식,vector_equation)에도 비슷한 꼴이 나온다 혹시 관련이??
의 선형결합이 나오는데 vector equation of a line(직선,line의 벡터방정식,vector_equation)에도 비슷한 꼴이 나온다 혹시 관련이??
오목볼록에는
10. tmp; 최대최소 ¶
fork to 최대최소,maximum_and_minimum
pl. maxima and minima
최대,maximum
https://mathworld.wolfram.com/Maximum.html
최소,minimum
{
최소,least도 만들?? Sub: 최소제곱,least_square { Up: 최소,least 제곱,square }
최대,maximum
https://mathworld.wolfram.com/Maximum.html
최소,minimum
{
최소,least도 만들?? Sub: 최소제곱,least_square { Up: 최소,least 제곱,square }
TBD. 최대와 최대값을, 최소와 최소값을 분리할 필요가 있을지? 일단 아래 몇줄은 분리한다고 가정하고 쓴 것, merge, or del ok
최대값,maximum_value
{
함수의 최대값 maximum value of a function =
정의역,domain 에서 정의된 함수,function
에서 정의된 함수,function ) 는 모든
는 모든 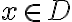 에 대해
에 대해
\le f(c))
인 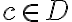 가 존재하면
가 존재하면 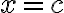 에서 최대값(maximum value)을 갖는다고 한다.[1]
에서 최대값(maximum value)을 갖는다고 한다.[1]
{
함수의 최대값 maximum value of a function =
정의역,domain
최소값,minimum_value
{
함수의 최소값 minimum value of a function =
정의역,domain 에서 정의된 함수,function
에서 정의된 함수,function ) 는 모든
는 모든 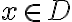 에 대해
에 대해
\ge f(c))
인 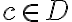 가 존재하면
가 존재하면 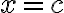 에서 최소값(minimum value)을 갖는다고 한다.[2]
에서 최소값(minimum value)을 갖는다고 한다.[2]
{
함수의 최소값 minimum value of a function =
정의역,domain
rel.
{
값,value이 붙으면 뭔가 뉘앙스차이가 발생하는지 아님 완전히 같은건지 chk.... 그리고 아래 페이지들이 필요한지...? tbd
최소,minimum = 최소값,minimum_value 표준어: 최솟값
}
{
값,value이 붙으면 뭔가 뉘앙스차이가 발생하는지 아님 완전히 같은건지 chk.... 그리고 아래 페이지들이 필요한지...? tbd
최대 최소는 adj, 최대값 최소값은 noun?
최대,maximum = 최대값,maximum_value 표준어: 최댓값최소,minimum = 최소값,minimum_value 표준어: 최솟값
}
이 둘은 가장 간단한 두 순서통계량,order_statistic { tmp see 통계량,statistic } 임.
이 둘을 통틀어 극값,extremum이라 함. (정의는 저 쪽을 참조)
이 둘을 통틀어 극값,extremum이라 함. (정의는 저 쪽을 참조)
관련표현: 최소화 최대화 극소화 극대화
https://mathworld.wolfram.com/LocalMaximum.html
극소,local_minimum
https://mathworld.wolfram.com/LocalMinimum.html
... 최대화,maximization 최소화,minimization ... QQQ 극대화 극소화는 최대화 최소화와 각각 동의어인지? 일단 극대/최대, 극소/최소는 calculus에서 의미가 다르긴 한데... CHK
극대,local_maximumhttps://mathworld.wolfram.com/LocalMaximum.html
극소,local_minimum
https://mathworld.wolfram.com/LocalMinimum.html
https://mathworld.wolfram.com/GlobalMaximum.html aka absolute_maximum
https://mathworld.wolfram.com/GlobalMinimum.html aka absolute_minimum
https://mathworld.wolfram.com/GlobalMinimum.html aka absolute_minimum
범위,range
구간,interval
경계,bound
유계,bounded
집합,set 등에서도 최대와 최소를 - 존재하는지, 존재한다면 값이 뭔지, ... etc - 생각할 수 있을텐데... 나중에 생각.
구간,interval
경계,bound
유계,bounded
집합,set 등에서도 최대와 최소를 - 존재하는지, 존재한다면 값이 뭔지, ... etc - 생각할 수 있을텐데... 나중에 생각.
변분법,variational_calculus 도 최대최소 관련인데 정확한 관계? TBW
{
aka variation method. 양자역학,quantum_mechanics에서 Hamiltonian의 풀이를 구하는 근사,approximation법 중 하나. 해밀토니안의 기대값,expected_value이 최저가 되도록 parameter 값을 최적화,optimization한다.![[https]](/123/imgs/https.png) src
src
aka variational calculus
aka variational method?
{
aka variation method. 양자역학,quantum_mechanics에서 Hamiltonian의 풀이를 구하는 근사,approximation법 중 하나. 해밀토니안의 기대값,expected_value이 최저가 되도록 parameter 값을 최적화,optimization한다.
![[https]](/123/imgs/https.png) src
srcaka variational calculus
aka variational method?
대충..... (공간에서?).. 뭔가가 최대나 최소(최대최소)가 되게 하는 경로,path나 곡선,curve등을 찾는???
(ex. 빛의 최소 소요 시간 - 페르마_원리,Fermat_principle .... // 빛,light 시간,time)
(ex. 빛의 최소 소요 시간 - 페르마_원리,Fermat_principle .... // 빛,light 시간,time)
기초 미적의 최대최소 찾기와 달리 범함수,functional를 대상으로??
사이클로이드,cycloid가 최단강하곡선brachistochrone?임을 증명하는 데 쓰이는데
mklink:
Lagrangian > 라그랑주_역학
Hamiltonian > 해밀턴_역학
오일러-라그랑주(Euler-Lagrange) 공식
Lagrangian > 라그랑주_역학
Hamiltonian > 해밀턴_역학
오일러-라그랑주(Euler-Lagrange) 공식
이 아니라 방정식인듯? 어디서보고공식이라썼더라.. 오일러-라그랑주_방정식,Euler-Lagrange_equation(writing)
극소곡면,minimal_surfacetmp links ko:
![[https]](/123/imgs/https.png) https://datascienceschool.net/02%20mathematics/04.05%20%EB%B3%80%EB%B6%84%EB%B2%95.html
https://datascienceschool.net/02%20mathematics/04.05%20%EB%B3%80%EB%B6%84%EB%B2%95.html
https://mathphysics.tistory.com/584
![[https]](/123/imgs/https.png) https://datascienceschool.net/02%20mathematics/04.05%20%EB%B3%80%EB%B6%84%EB%B2%95.html
https://datascienceschool.net/02%20mathematics/04.05%20%EB%B3%80%EB%B6%84%EB%B2%95.htmlhttps://mathphysics.tistory.com/584
Twins:
https://www.scienceall.com/변분법calculus-of-variations/
![[https]](/123/imgs/https.png) 수학백과: 변분법
수학백과: 변분법
 Calculus_of_variations
Calculus_of_variations
 변분법
변분법
 변분법
변분법
https://mathworld.wolfram.com/CalculusofVariations.html
https://planetmath.org/calculusofvariations
https://encyclopediaofmath.org/wiki/Variational_calculus
}
https://www.scienceall.com/변분법calculus-of-variations/
![[https]](/123/imgs/https.png) 수학백과: 변분법
수학백과: 변분법https://mathworld.wolfram.com/CalculusofVariations.html
https://planetmath.org/calculusofvariations
https://encyclopediaofmath.org/wiki/Variational_calculus
}
미니맥스 minimax ... pagename TBD, kms minimax => https://www.kms.or.kr/mathdict/list.html?key=ename&keyword=minimax 보면 보통 '최대최소' ?
{
 최소극대화
최소극대화
{
kms words:
minimax approximation 최소최대근사값
minimax method 최대최소법
minimax theorem 최대최소정리
(최대최소와 최소최대가 혼용되는 이유가? - 2023-01-28 영어 단어순으로 직역하면 최소최대인데, 보통 언어에선 '소대'보다는 '대소' 순으로 많이 쓰이기 때문인 듯?)
}
minimax approximation 최소최대근사값
minimax method 최대최소법
minimax theorem 최대최소정리
(최대최소와 최소최대가 혼용되는 이유가? - 2023-01-28 영어 단어순으로 직역하면 최소최대인데, 보통 언어에선 '소대'보다는 '대소' 순으로 많이 쓰이기 때문인 듯?)
}
arguments of the maxima, arg max, argmax
함수,function에서, 함수값이 최대가 되는 정의역,domain의 점(point)이나 원소(element)(들). (wpen)
출력이 최대(maximum)가 되는 입력(input, argument)을 찾으므로 이런 이름?
함수,function에서, 함수값이 최대가 되는 정의역,domain의 점(point)이나 원소(element)(들). (wpen)
출력이 최대(maximum)가 되는 입력(input, argument)을 찾으므로 이런 이름?
정의가
argmax는 global_maximum (= absolute_maximum) 관련이고
argmin은 global_minimum (= absolute_minimum) 관련임. chkout planetmath.
argmax는 global_maximum (= absolute_maximum) 관련이고
argmin은 global_minimum (= absolute_minimum) 관련임. chkout planetmath.
비슷한 방식으로 arg min, argmin도 정의 가능.
최적화,optimization
최대 최소 max min 등의 이름이 들어간 페이지들 (나중에 sub related 등으로...)
{
최대가능도,maximum_likelihood
최대가능도추정,maximum_likelihood_estimation,MLE
최소항과_최대항,minterm_and_maxterm
최대최소정리,extreme_value_theorem,EVT
}
에는 오차,error, ..., (뭔가 나쁜 정도를 측정하는 함수) 같은 걸 만들어 놓고 이것을 최소화하는 기법이 자주 쓰이는 듯 한데.
심층학습,deep_learning 기계학습,machine_learning최대 최소 max min 등의 이름이 들어간 페이지들 (나중에 sub related 등으로...)
{
최대가능도,maximum_likelihood
최대가능도추정,maximum_likelihood_estimation,MLE
최소항과_최대항,minterm_and_maxterm
최대최소정리,extreme_value_theorem,EVT
}
꼭대기(apex)를 찾으려면 어떻게?
함수의 특정 한 곳 근방에서 최대값을 찾는 방법으로 뉴턴 최적화(Newton optimization)가 있다
기타등등 tbw.
함수의 특정 한 곳 근방에서 최대값을 찾는 방법으로 뉴턴 최적화(Newton optimization)가 있다
기타등등 tbw.
단어, 표현 (kms)
absolute minimum 최대(값)
absolute minimum 최소(값)
local maximum 극대
local minimum 극소
absolute minimum 최대(값)
absolute minimum 최소(값)
local maximum 극대
local minimum 극소
monotonic function 단조함수
monotonic sequence 단조수열
monotonicity 단조성
monotonic sequence 단조수열
monotonicity 단조성
local=relative vs global=absolute 라고 적는 영어 표현이 한국어 표현보다 더 직관적이라는 의견[4]에 동의하는 바이며 차라리 '극-' 보다는 '국소'가 더 와닿는다.
(Misc)
TBW: 비교(using conditional statement)없이 절대값,absolute_value들어간 수식만으로 max, min 구하는 식, 그리고 증명.
{
chk:
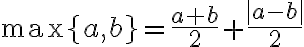
뭐 이런것들...
tmp links:
https://math.stackexchange.com/questions/685509/show-max-a-b-frac12aba-b
https://math.stackexchange.com/questions/258934/how-to-prove-this-simple-statement-max-a-b-frac12aba-b
}
TBW: 비교(using conditional statement)없이 절대값,absolute_value들어간 수식만으로 max, min 구하는 식, 그리고 증명.
{
chk:
tmp links:
https://math.stackexchange.com/questions/685509/show-max-a-b-frac12aba-b
https://math.stackexchange.com/questions/258934/how-to-prove-this-simple-statement-max-a-b-frac12aba-b
}
순서,order... 순서론,order_theory 에서는 원소,element에 대해 최대최소를 이렇게 씀
https://encyclopediaofmath.org/wiki/Maximum_and_minimum_points
https://encyclopediaofmath.org/wiki/Maximization_and_minimization_of_functions
https://encyclopediaofmath.org/wiki/Maximum_and_minimum_points
https://encyclopediaofmath.org/wiki/Maximization_and_minimization_of_functions
11. 증가감소 ¶
curr at txtfile =증가감소
///////// 이하 꼭 미적 관련 내용은 아닌데, 위의 오목볼록 최대최소 와 유사한 성격의 페이지라, 일단 여기에 적음 ////////////
13. 열린닫힌,open_and_closed ¶
열림 openness ??
닫힘 closedness ? closure ?
half-open = half-closed 이건 내가 본건 다 그렇던데(구간,interval등등) ..항상?
닫힘 closedness ? closure ?
half-open = half-closed 이건 내가 본건 다 그렇던데(구간,interval등등) ..항상?
14. 홀짝 홀짝성 패리티 패러티 parity ¶
번역? pagename?
홀짝성,parity - maybe?
패리티 - 패러티 ...가 더 정확한 발음 같은데.
패러티
짝홀값 from![[https]](/123/imgs/https.png) 수학산책: 컴퓨터의 오류정정
수학산책: 컴퓨터의 오류정정
and ....?
홀짝성,parity - maybe?
패리티 - 패러티 ...가 더 정확한 발음 같은데.
패러티
짝홀값 from
![[https]](/123/imgs/https.png) 수학산책: 컴퓨터의 오류정정
수학산책: 컴퓨터의 오류정정and ....?
뜻이 여러 분야에 많아서 정의를 간단히 적기 쉽지 않음.
정수의 parity
정수,integer를 2로 나누어 떨어지면/1이 남으면 각각 ...
짝수 even_number
홀수 odd_number
mklink
나눗셈,division > 정수나눗셈 integer_division or Euclidean_division
정수,integer를 2로 나누어 떨어지면/1이 남으면 각각 ...
짝수 even_number
홀수 odd_number
mklink
나눗셈,division > 정수나눗셈 integer_division or Euclidean_division
함수의 parity
함수,function:
짝함수 even_function = 우함수
홀함수 odd_function = 기함수
https://encyclopediaofmath.org/wiki/Even_function
https://encyclopediaofmath.org/wiki/Odd_function
https://planetmath.org/evenandoddfunctions
https://mathworld.wolfram.com/EvenFunction.html
https://mathworld.wolfram.com/OddFunction.html
 홀함수와_짝함수
홀함수와_짝함수
 Even_and_odd_functions
Even_and_odd_functions
함수,function:
짝함수 even_function = 우함수
홀함수 odd_function = 기함수
https://encyclopediaofmath.org/wiki/Even_function
https://encyclopediaofmath.org/wiki/Odd_function
https://planetmath.org/evenandoddfunctions
https://mathworld.wolfram.com/EvenFunction.html
https://mathworld.wolfram.com/OddFunction.html
permutation의 parity
순열,permutation, 치환,permutation: curr see 순열
순열
짝치환 짝순열 even_permutation
홀치환 홀순열 odd_permutation
 순열의 홀짝성
순열의 홀짝성
// .... parity of permutation
parity of permutation
순열,permutation, 치환,permutation: curr see
짝치환 짝순열 even_permutation
홀치환 홀순열 odd_permutation
// ....
parity_check -검사
parity check
 parity check
parity check
Up: 검사,check ... 검사 check
검사 check  검사 check // 검사에는 검사,inspection의 뜻도.
검사 check // 검사에는 검사,inspection의 뜻도.
parity check
Up: 검사,check ...
parity_bit
parity bit
 parity_bit
parity_bit
http://foldoc.org/parity bit (short)
 패리티_비트
패리티_비트
 Parity_bit
Parity_bit
한계: (오류를 찾을 수만 있을 뿐) 수정까지는 할 수 없다
rel: data_transmission ... curr at 통신,communication, error_detection error_correction ... curr at 오류,error
// parity bit ... parity bit
parity bit  parity bit
parity bit
parity bit
http://foldoc.org/parity bit (short)
한계: (오류를 찾을 수만 있을 뿐) 수정까지는 할 수 없다
rel: data_transmission ... curr at 통신,communication, error_detection error_correction ... curr at 오류,error
// parity bit ...
parity_error
parity error
wt x 2024-03
http://foldoc.org/parity error (short)
Up: 오류,error
// parity error ... parity error
parity error  parity error
parity error
parity error
wt x 2024-03
http://foldoc.org/parity error (short)
Up: 오류,error
// parity error ...
longitudinal_parity
{
longitudinal parity
http://foldoc.org/longitudinal parity
} // longitudinal parity .... longitudinal parity
longitudinal parity  longitudinal parity
longitudinal parity
http://foldoc.org/paritylongitudinal parity
http://foldoc.org/longitudinal parity
} // longitudinal parity ....
15. 미적분학이 아닌 calculi ¶
해석학,analysis의 일부이며 '미적분학' '미분적분학'으로 번역되는 그 calculus가 아닌 calculus들이 많은데 pagename 결정을 위해 번역 문제를 생각해봐야.
'미적분'과 변분법,variational_calculus 밖에서 쓰이는
'계산, 계산법, 대수'으로 번역되는 calculus에 대해선 현재 형식체계,formal_system 참조.
'계산, 계산법, 대수'으로 번역되는 calculus에 대해선 현재 형식체계,formal_system 참조.
둘다 calculus로 불리는 원인? 이유?
아마 이 링크가 감잡는데 도움이?
{
https://compcalc.github.io/
https://news.ycombinator.com/item?id=27004278
https://encyclopediaofmath.org/wiki/Calculus
}
아마 이 링크가 감잡는데 도움이?
{
https://compcalc.github.io/
https://news.ycombinator.com/item?id=27004278
https://encyclopediaofmath.org/wiki/Calculus
}
2022-02-03 Calculus의 분류?
https://ncatlab.org/nlab/show/differential calculus 보면 여러 calculus 중에
 database분야에 calculus로는
database분야에 calculus로는  관계해석relational_calculus이 있다. (저기선 calculus를 '해석'으로 번역. Relational algebra는 '관계대수'로 번역하지만.)
관계해석relational_calculus이 있다. (저기선 calculus를 '해석'으로 번역. Relational algebra는 '관계대수'로 번역하지만.)
https://ncatlab.org/nlab/show/differential calculus 보면 여러 calculus 중에
- infinitesimal_calculus 가 있고 이건 다음 둘로 나뉘며 서로 미적분학의기본정리,FTC로 연결 // infinitesimal
- differential_calculus // 번역한다면 분명 '미분(학)'
- 변분법,variational_calculus : non-finite (뜻? infinite라고 하지 않고 이렇게 쓴 이유?) dimensional_spaces에서 differential_calculus 를 이렇게도 부른다
- 비가환미분학? noncommutative_differential_calculus // noncommutativity - rel. 교환법칙,commutativity#s-2
- 변분법,variational_calculus : non-finite (뜻? infinite라고 하지 않고 이렇게 쓴 이유?) dimensional_spaces에서 differential_calculus 를 이렇게도 부른다
- integral_calculus // 번역한다면 분명 '적분(학)'
- differential_calculus // 번역한다면 분명 '미분(학)'
2023-01-11
논리학(논리,logic)분야의 calculus들은 대개 -논리 로 번역되는듯 ... (-연산 으로도 번역됨)
왜 그러냐면 아마도 저기선 _calculus 가 _logic 와 동의어인 경우가 많은 듯 한데.
ex.
논리학(논리,logic)분야의 calculus들은 대개 -논리 로 번역되는듯 ... (-연산 으로도 번역됨)
왜 그러냐면 아마도 저기선 _calculus 가 _logic 와 동의어인 경우가 많은 듯 한데.
ex.
minimal_logic = minimal_calculus (curr at 논리,logic#s-4) ...  Minimal_logic ... "Minimal logic, or minimal calculus"
Minimal_logic ... "Minimal logic, or minimal calculus"
propositional_calculus (writing)
 Calculus_(disambiguation)
Calculus_(disambiguation)
propositional_calculus (writing)
번역은 아마 명제연산 or 명제논리?
curr see Well-formed_formula#Propositional_calculus and
Well-formed_formula#Propositional_calculus and  Propositional_calculus ... "also called propositional_logic"
Propositional_calculus ... "also called propositional_logic"
... propositional calculus를 보면 '명제 연산, 명제산, 명제계산 ... ' 등 제각각.
propositional calculus를 보면 '명제 연산, 명제산, 명제계산 ... ' 등 제각각.
 명제_논리
명제_논리
찾아보니 이미 명제논리,propositional_logic 페이지 존재.
logical_calculuscurr see
...
찾아보니 이미 명제논리,propositional_logic 페이지 존재.
-calculus를 기계적으로 -논리 라 번역한다면 이건 '논리적논리 or 논리논리'라고 해야 하는 불상사가 생긴다. 번역한다면 '논리연산'? 자주 쓰이는 표현은 아님.
https://encyclopediaofmath.org/wiki/Logical_calculus
... logical calculus
logical calculus
https://encyclopediaofmath.org/wiki/Logical_calculus
...
----
- [1] 서울대기초수학학습교재 p92
- [2] 서울대기초수학학습교재 p92
- [3] https://suhak.tistory.com/331
- [4] https://m.blog.naver.com/piry777/100163196533


![[http]](/123/imgs/http.png)